【题目】解不等式组 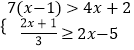 将其解集在数轴上表示出来,并写出这个不等式组的整数解.
将其解集在数轴上表示出来,并写出这个不等式组的整数解. ![]()
参考答案:
【答案】解:解不等式①,得:x>3, 解不等式②,得:x≤4,
∴不等式组的解集为3<x≤4,
解集表示在数轴上如下:
则其整数解为4
【解析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【考点精析】解答此题的关键在于理解不等式的解集在数轴上的表示的相关知识,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈,以及对一元一次不等式组的解法的理解,了解解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax-2ax-3a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC交于点M,且PM=
 AB.
AB.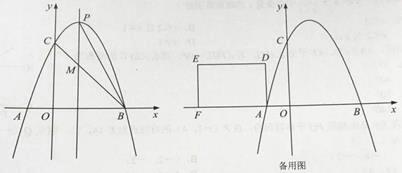
(1)求抛物线的解析式;
(2)点K是x轴正半轴上一点,点A、P关于点K的对称点分别为 、
、  ,连接
,连接 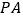 、
、 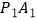 ,若
,若 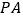
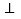
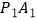 ,求点K的坐标;
,求点K的坐标;
(3)矩形ADEF的边AF在x轴负半轴上,边AD在第二象限,AD=2,DE=3.将矩形ADEF沿x轴正方向平移t(t>0)个单位,直线AD、EF分别交抛物线于G、H.问:是否存在实数t,使得以点D、F、G、H为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,说明理由. -
科目: 来源: 题型:
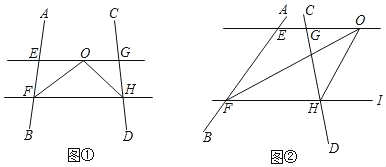
查看答案和解析>>【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么
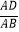 的值是 .
的值是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B,C在同一直线上,线段AB=10cm且AC=6cm,M是AB的中点, N是AC的中点,则线段MN的长度是_________.
-
科目: 来源: 题型:
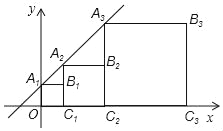
查看答案和解析>>【题目】如图,正方形A1B1C1D1、A2B2C2D2……按照如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),B3(7,4)则B2018的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
相关试题

