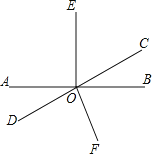
【题目】如图,已知直线AB与直线CD相交于点O,∠BOE=90°,FO平分∠BOD,∠BOC:∠AOC=1:3.
(1)求∠DOE、∠COF的度数.
(2)若射线OF、OE同时绕O点分别以2°/s、4°/s的速度,顺时针匀速旋转,当射线OE、OF的夹角为90°时,两射线同时停止旋转.设旋转时间为t,试求t值.
参考答案:
【答案】(1)135,112.5°;(2)33.75.
【解析】
(1)根据平角的定义和已知条件可求∠BOC的度数,根据对顶角相等可求∠AOD的度数,根据角的和差关系可求∠DOE的度数,根据平角的定义和角平分线的定义可求∠DOF的度数,再根据平角的定义求得∠COF的度数;
(2)先求出∠EOF的度数,再根据射线OE、OF的夹角为90,列出方程求解即可.
解:(1)∵∠BOC:∠AOC=1:3,
∴∠BOC=180°×![]() =45°,
=45°,
∴∠AOD=45°,
∵∠BOE=90°,
∴∠AOE=90°,
∴∠DOE=45°+90°=135°,
∠BOD=180°-45°=135°,
∵FO平分∠BOD,
∴∠DOF=∠BOF=67.5°,
∴∠COF=180°-67.5°=112.5°.
(2)∠EOF=90°+67.5°=157.5°,
依题意有
4t-2t=157.5-90,
解得t=33.75.
故t值为33.75.
故答案为:(1)135,112.5°;(2)33.75.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个有50个奇数排成的数阵,用如图所示的框去框住四个数,并求出这四个数的和,在下列给出的备选答案中,有可能是这四个数的和的是( )
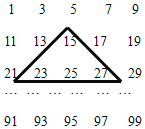
A. 114 B. 122 C. 220 D. 84
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行摸排游戏,现有三张形状大小完全相同的牌,正面分别标有数字2,3,5,将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法写出所有可能的结果;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、P是数轴上的三个点,P是AB的中点,A、B所对应的数值分别为-20和40.
(1)试求P点对应的数值;若点A、B对应的数值分别是a和b,试用a、b的代数式表示P点在数轴上所对应的数值;
(2)若A、B、P三点同时一起在数轴上做匀速直线运动,A、B两点相向而行,P点在动点A和B之间做触点折返运动(即P点在运动过程中触碰到A、B任意一点就改变运动方向,向相反方向运动,速度不变,触点时间忽略不计),直至A、B两点相遇,停止运动.如果A、B、P运动的速度分别是1个单位长度/s,2个单位长度/s,3个单位长度/s,设运动时间为t.
①求整个运动过程中,P点所运动的路程.
②若P点用最短的时间首次碰到A点,且与B点未碰到,试写出该过程中,P点经过t秒钟后,在数轴上对应的数值(用含t的式子表示);
③在②的条件下,是否存在时间t,使P点刚好在A、B两点间距离的中点上,如果存在,请求出t值,如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,则下列说法不正确的是( )
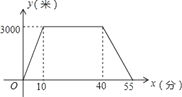
A. 小刘家与超市相距3000米 B. 小刘去超市途中的速度是300米/分
C. 小刘在超市逗留了30分钟 D. 小刘从超市返回家比从家里去超市的速度快
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图描述了某汽车在行驶过程中速度与时间的关系,下列说法中正确的是________.(填序号)
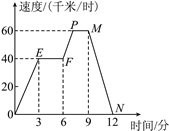
①第3分钟时,汽车的速度是40千米/时;
②第12分钟时,汽车的速度是0千米/时;
③从第3分钟到第6分钟,汽车行驶了120千米;
④从第9分钟到第12分钟,汽车的速度从60千米/时减小到0千米/时.
相关试题

