搜索
【题目】点P关于x轴的对称点为（2，-1），那么点P的坐标是（ ）
A.（-2，1）B.（1，-2）C.（-1，-2）D.（2，1）
参考答案：
【答案】D
【解析】
根据平面直角坐标系中两个点关于x轴对称的坐标特点，即可求解本题．
解：∵点P关于x轴的对称点为（2，-1），
∴P（2,1）；
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
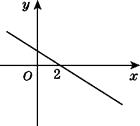
A.x<2
B.x>2
C.x<5
D.x>5 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2<kx+b<1的解集为
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的
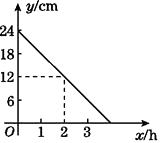
高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图提供的信息,解答下列问题:
（1）蜡烛燃烧时y与x之间的函数表达式为
（2）蜡烛从点燃到燃尽所用的时间为. -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
上课时李老师提出这样一个问题：对于任意实数x，关于x的不等式x2﹣2x﹣1﹣a＞0恒成立，求a的取值范围．
小捷的思路是：原不等式等价于x2﹣2x﹣1＞a，设函数y1=x2﹣2x﹣1，y2=a，画出两个函数的图象的示意图，于是原问题转化为函数y1的图象在y2的图象上方时a的取值范围．
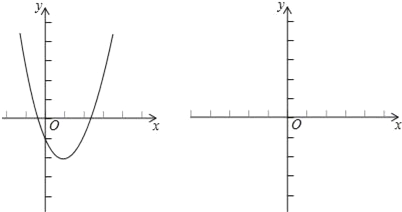
请结合小捷的思路回答：
对于任意实数x，关于x的不等式x2﹣2x﹣1﹣a＞0恒成立，则a的取值范围是 ．
参考小捷思考问题的方法，解决问题：
关于x的方程x﹣4=
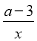在0＜a＜4范围内有两个解，求a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】数学小组的两位同学准备测量两幢教学楼之间的距离，如图，两幢教学楼AB和CD之间有一景观池（AB⊥BD，CD⊥BD），一同学在A点测得池中喷泉处E点的俯角为42°，另一同学在C点测得E点的俯角为45°（点B，E，D在同一直线上），两个同学已经在学校资料室查出楼高AB=15m，CD=20m，求两幢教学楼之间的距离BD．
（结果精确到0.1m，参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=﹣2x2+4x﹣3，如果y随x的增大而减小，那么x的取值范围是（ ）
A.x≥1
B.x≥0
C.x≥﹣1
D.x≥﹣2
相关试题
