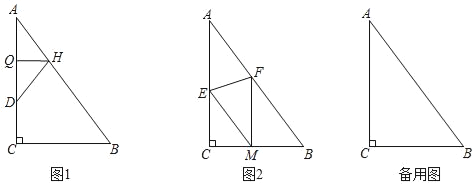
【题目】在△ABC中,∠ACB=90°,AB=25,BC=15.
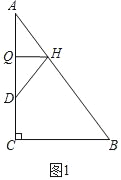
(1)如图1,折叠△ABC使点A落在AC边上的点D处,折痕交AC、AB分别于Q、H,若S△ABC=9S△DHQ,则HQ= .
(2)如图2,折叠△ABC使点A落在BC边上的点M处,折痕交AC、AB分别于E、F.若FM∥AC,求证:四边形AEMF是菱形;
(3)在(1)(2)的条件下,线段CQ上是否存在点P,使得△CMP和△HQP相似?若存在,求出PQ的长;若不存在,请说明理由.
参考答案:
【答案】(1)5;(2)证明见解析;(3)QP的值为![]() 或10或
或10或![]() .
.
【解析】
(1)利用勾股定理求出AC,设HQ=x,根据S△ABC=9S△DHQ,构建方程即可解决问题;
(2)想办法证明四边相等即可解决问题;
(3)设AE=EM=FM=AF=4m,则BM=3m,FB=5m,构建方程求出m的值,分两种情形分别求解即可解决问题.
解:(1)如图1中,
在△ABC中,∵∠ACB=90°,AB=25,BC=15,
∴AC=![]() =20,设HQ=x,
=20,设HQ=x,
∵HQ∥BC,
∴![]() ,
,
∴AQ=![]() x,
x,
∵S△ABC=9S△DHQ,
∴![]() ×20×15=9×
×20×15=9×![]() ×x×
×x×![]() x,
x,
∴x=5或﹣5(舍弃),
∴HQ=5,
故答案为5.
(2)如图2中,
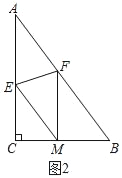
由翻折不变性可知:AE=EM,AF=FM,∠AFE=∠MFE,
∵FM∥AC,
∴∠AEF=∠MFE,
∴∠AEF=∠AFE,
∴AE=AF,
∴AE=AF=MF=ME,
∴四边形AEMF是菱形.
(3)如图3中,
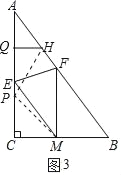
设AE=EM=FM=AF=4m,则BM=3m,FB=5m,
∴4m+5m=25,
∴m=![]() ,
,
∴AE=EM=![]() ,
,
∴EC=20﹣![]() =
=![]() ,
,
∴CM=![]() ,
,
∵QG=5,AQ=![]() ,
,
∴QC=![]() ,设PQ=x,
,设PQ=x,
当![]() 时,△HQP∽△MCP,
时,△HQP∽△MCP,
∴![]() ,
,
解得:x=![]() ,
,
当![]() =时,△HQP∽△PCM,
=时,△HQP∽△PCM,
∴![]()
解得:x=10或![]() ,
,
经检验:x=10或![]() 是分式方程的解,且符合题意,
是分式方程的解,且符合题意,
综上所,满足条件长QP的值为![]() 或10或
或10或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则以下结论同时成立的是



A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OADB的顶点A,B的坐标分别为A(﹣6,0),B(0,4).过点C(﹣6,1)的双曲线y=
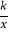 (k≠0)与矩形OADB的边BD交于点E.
(k≠0)与矩形OADB的边BD交于点E.(1)填空:OA= ,k= ,点E的坐标为 ;
(2)当1≤t≤6时,经过点M(t﹣1,﹣
 t2+5t﹣
t2+5t﹣ )与点N(﹣t﹣3,﹣
)与点N(﹣t﹣3,﹣ t2+3t﹣
t2+3t﹣ )的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣
)的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣ x2+bx+c的顶点.
x2+bx+c的顶点.①当点P在双曲线y=
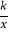 上时,求证:直线MN与双曲线y=
上时,求证:直线MN与双曲线y=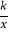 没有公共点;
没有公共点;②当抛物线y=﹣
 x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
x2+bx+c与矩形OADB有且只有三个公共点,求t的值;③当点F和点P随着t的变化同时向上运动时,求t的取值范围,并求在运动过程中直线MN在四边形OAEB中扫过的面积.

-
科目: 来源: 题型:
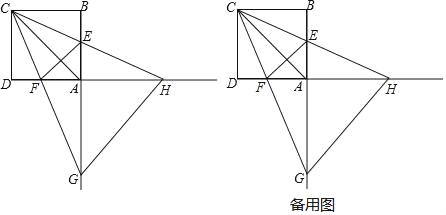
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知A(2,0),B(1,-1),将线段OA绕点O逆时针旋转,旋转角为
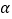 (0°<
(0°<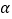 <135°).记点A的对应点为A1,若点A1与点B的距离为
<135°).记点A的对应点为A1,若点A1与点B的距离为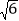 ,则
,则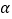 为( ).
为( ).A. 30° B. 45° C. 60° D. 90°
相关试题

