【题目】如图,已知反比例函数 ![]() 的图象与一次函数
的图象与一次函数 ![]() 的图象交于点A(1,4)、点B(-4,n).
的图象交于点A(1,4)、点B(-4,n).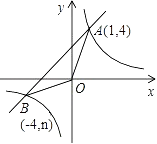
(1)求 ![]() 和
和 ![]() 的值;
的值;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量 ![]() 的取值范围.
的取值范围.
参考答案:
【答案】
(1)解:把A点(1,4)分别代入反比例函数y=![]() ,一次函数y=x+b,
,一次函数y=x+b,
得k=1×4,1+b=4,解得k=4,b=3,
∴反比例函数的解析式是y=![]() ,一次函数解析式是y=x+3;
,一次函数解析式是y=x+3;
(2)解:如图,设直线y=x+3与y轴的交点为C,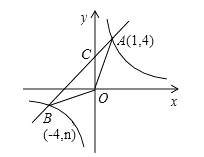
当x=-4时,y=-1,∴B(-4,-1),当x=0时,y=+3,∴C(0,3),
∴S△AOB=S△AOC+S△BOC=×3×4+×3×1=15/2
(3)解:∵B(-4,-1),A(1,4),
∴根据图象可知:当x>1或-4<x<0时,一次函数值大于反比例函数值.
【解析】(1)将点A的坐标分别代入两函数解析式,求出k、b的值,即可求出函数解析式。
(2)先求出点B的坐标,再求出直线AB与y轴的交点C的坐标,再根据S△AOB=S△AOC+S△BOC计算即可得出结果。
(3)观察直线x=-4、y轴、直线x=1这三条直线将两图像分成四部分,由图像观察一次函数的图像高于反比例函数的图像,写出取值范围即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2
 =(1+
=(1+ )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b =(m+n
=(m+n )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b =m2+2n2+2mn
=m2+2n2+2mn ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b 的式子化为平方式的方法。
的式子化为平方式的方法。
请我仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b =(m+n
=(m+n )2,用含m、n的式子分别表示a、b,得a=________, b=___________.
)2,用含m、n的式子分别表示a、b,得a=________, b=___________.(2)若a+4
 =(m+n
=(m+n )2,且a、m、n均为正整数,求a的值。
)2,且a、m、n均为正整数,求a的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.
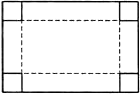
-
科目: 来源: 题型:
查看答案和解析>>【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】根据绍兴市某风景区的旅游信息:
旅游人数
收费标准
不超过30人
人均收费80元
超过30人
每增加1人,人均收费降低1元,但人均收费不低于55元
A公司组织一批员工到该风景区旅游,支付给旅行社2800元.A公司参加这次旅游的员工有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数
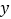 (件)与价格
(件)与价格  (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于
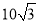 cm2?
cm2?
相关试题

