【题目】甲、乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h), y甲、y乙与x之间的函数图像如图所示,结合图像解答下列问题: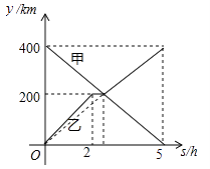
(1)甲车的速度是km/h,乙车休息了 h;
(2)求乙车与甲车相遇后y乙与x的函数解析式,并写出自变量x的取值范围;
(3)当甲车出发多少小时后,两车相距80km?
参考答案:
【答案】
(1)解:80,0.5
(2)解:设y乙与x的函数解析式为y乙=kx﹢b,把(2.5,200).(5,400)代入,得:
![]()
解得: ![]()
y乙=80x(2.5≤x≤5)
(3)解:相遇前:100x﹢80x﹢80=400,解得x= ![]() ;
;
相遇后:80x﹢200﹢80(x﹣2.5)=400+80,解得x=3.
综上可知,x= ![]() 或x=3
或x=3
【解析】(1)根据图像可知甲车共行驶了5小时,400km,求出甲车的速度;乙车共行驶了2小时,200km,求出乙车的速度和行驶的时间,由乙车休息和行驶共计5小时,求出乙车休息的时间;(2)把(2.5,200).(5,400)代入,求出乙车与甲车相遇后y乙与x的函数解析式,写出自变量x的取值范围;(3)根据相遇前和相遇后,分别求出两车相距80km的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
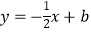 的图像与x轴、y轴分别交于点A、B,与函数
的图像与x轴、y轴分别交于点A、B,与函数 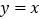 的图像交于点M,点M的横坐标为2.
的图像交于点M,点M的横坐标为2.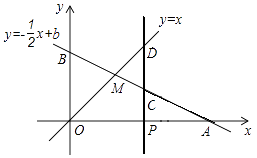
(1)求点A的坐标;
(2)在x轴上有一点动点P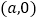 (其中
(其中 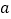 >2),过点P作x轴的垂线,分别交函数
>2),过点P作x轴的垂线,分别交函数 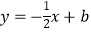 和
和 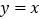 的图像于点C、D,且OB=2CD,求
的图像于点C、D,且OB=2CD,求 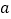 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG.
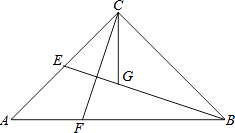
(1)求证:CF=BG;
(2)延长CG交AB于点H,判断点G是否在线段AB的垂直平分线上?并说明理由.
(3)过点A作AD⊥AB交BE的延长线于点D,请证明:CF=2DE. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个容量为50的样本中,数据的最大值是123,最小值是45,若取每组终点值与起点值的差为10,则该样本可以分( )
A.5组或6组
B.6组或7组
C.7组或8组
D.8组或9组 -
科目: 来源: 题型:
查看答案和解析>>【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A.得分在70~80分之间的人数最多
B.该班的总人数为40
C.得分在90~100分之间的人数最少
D.及格(≥60分)人数是26
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2-2mx+25是完全平方式,则m的值为( )
A. 5B. ±5C. 10D. ±10
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
【问题情境】金老师给“数学小达人”小明和小军提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC.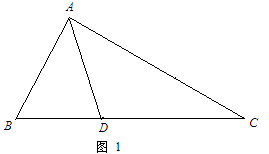
【证明思路】小明的证明思路是:如图2,在AC上截取AE=AB,连接DE.……
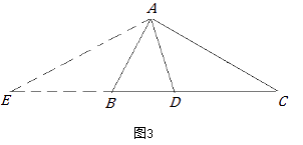
小军的证明思路是:如图3,延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE.……
(1)请你从他们的思路中,任意选择一种思路继续完成下一步的证明.
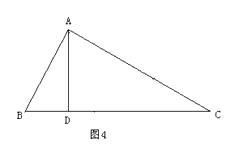
(2)【变式探究】如图4,金老师把“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变,那么AB+BD=AC还成立吗?若成立,请证明;若不成立,写出正确结论,并说明理由.
(3)【迁移拓展】如图5,△ABC中,∠B=2∠C.求证:AC2—AB2=AB×BC.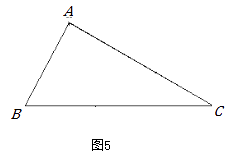
相关试题

