【题目】在如图所示的七边形ABCDEFG中,∠1、∠2、∠3、∠4 四个角的外角和为180°,∠5 的外角为60°,BP、DP 分别平分∠ABC、∠CDE,则∠BPD 的度数是( )

A. 130° B. 120° C. 110° D. 100°
参考答案:
【答案】B
【解析】分析:根据邻补角互补得出,∠1+∠2+∠3+∠4=4×180°﹣180°=540°,∠5=120°,利用多边形内角和定理求出∠ABC+∠CDE=240°,根据角平分线定义得出∠CBP+∠CDP=120°,然后根据四边形内角和定理求出∠BPD 的度数.
详解:∵∠1、∠2、∠3、∠4 四个角的外角和为180°,∠5 的外角为60°,∴∠1+∠2+∠3+∠4=4×180°﹣180°=540°,∠5=120°,∴∠ABC+∠CDE=(7﹣2)×180°﹣540°﹣120°=240°.
∵BP、DP 分别平分∠ABC、∠CDE,∴∠CBP+∠CDP=![]() (∠ABC+∠CDE)=120°,∴∠BPD=360°﹣∠5﹣(∠CBP+∠CDP)=360°﹣120°﹣120°=120°.
(∠ABC+∠CDE)=120°,∴∠BPD=360°﹣∠5﹣(∠CBP+∠CDP)=360°﹣120°﹣120°=120°.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在查阅大数学家高斯的资料时,知道了高斯如何求1+2+3+…+100.小明于是对从1开始连续奇数的和进行了研究,发现如下式子:
第1个等式:
 ;第2个等式:
;第2个等式:  ;第3个等式:
;第3个等式: 
探索以上等式的规律,解决下列问题:
(1)


 ;
;(2)完成第
 个等式的填空:
个等式的填空:  ;
;(3)利用上述结论,计算51+53+55+…+109 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平整的地面上,用若干个完全相同的棱长为10 cm的小正方体堆成一个几何体.
(1)现已给出这个几何体的俯视图(如图②),请你画出这个几何体的主视图与左视图;
(2)若现在你手头还有一些相同的小正方体,如果保持这个几何体的主视图和俯视图不变.
①在图①所示的几何体中最多可以再添加几个小正方体?
②在图①所示的几何体中最多可以拿走几个小正方体?
③在②的情况下,把这个几何体放置在墙角,如图③所示是此时这个几何体放置的俯视图,若给这个几何体表面喷上红漆,则需要喷漆的面积最少是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线
 上有三点
上有三点 、
、 、
、 ,满足
,满足 ,
,  ,
,  ,点
,点 从点
从点 出发,沿
出发,沿 方向以
方向以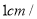 秒的速度匀速运动,点
秒的速度匀速运动,点 从点
从点 出发在线段
出发在线段 上向点
上向点 匀速运动,两点同时出发,当点
匀速运动,两点同时出发,当点 运动到点
运动到点 时,点
时,点 、
、 停止运动.
停止运动.(1)若点
 运动速度为
运动速度为 秒,经过多长时间
秒,经过多长时间 、
、 两点相遇?
两点相遇?(2)当
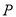 在线段
在线段 上且
上且 时,点
时,点 运动到的位置恰好是线段
运动到的位置恰好是线段 的三等分点,
的三等分点,求点
 的运动速度;
的运动速度;(3)当点
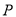 运动到线段
运动到线段 上时,分别取
上时,分别取 和
和 的中点
的中点 、
、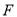 ,求
,求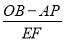 的值.
的值.
-
科目: 来源: 题型:
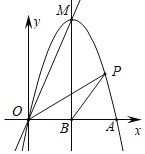
查看答案和解析>>【题目】如图,抛物线y=ax2+bx(a≠0)交x轴正半轴于点A,直线y=2x经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.
(1)求M点的坐标及a,b的值;
(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m,△OBP的面积为S,当m为多少时,s=
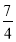 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.

相关试题

