【题目】小明同学在查阅大数学家高斯的资料时,知道了高斯如何求1+2+3+…+100.小明于是对从1开始连续奇数的和进行了研究,发现如下式子:
第1个等式: ![]() ;第2个等式:
;第2个等式: ![]() ;第3个等式:
;第3个等式: ![]()
探索以上等式的规律,解决下列问题:
(1) ![]()
![]()
![]() ;
;
(2)完成第![]() 个等式的填空:
个等式的填空: ![]() ;
;
(3)利用上述结论,计算51+53+55+…+109 .
参考答案:
【答案】(1)25;(2)2n-1;(3)2400.
【解析】
(1)根据题目中的规律,写出答案即可.
(2)根据题目中的规律,反推答案即可.
(3)利用规律通式,代入计算即可.
(1) 由题意规律可以得,连续奇数的和为中间相的平方,
所以![]()
![]() .
.
(2)设最后一项为x,由题意可推出: ![]() ,x=2n-1.
,x=2n-1.
(3)根据上述结论, 51+53+55+…+109=(1+3+5+···+109)-( 1+3+5+···+49)=552-252=2400.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10
 km,一艘货轮从B港口沿如图所示的BC方向航行4
km,一艘货轮从B港口沿如图所示的BC方向航行4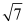 km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
A.8
 B.9
B.9 C.6
C.6 D.7
D.7
-
科目: 来源: 题型:
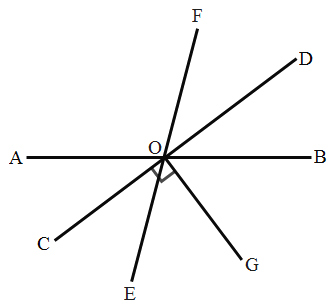
查看答案和解析>>【题目】如图,直线
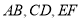 相交于点
相交于点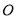 ,
,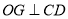 .
.
(1)已知
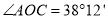 ,求
,求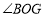 的度数;
的度数;(2)如果
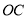 是
是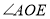 的平分线,那么
的平分线,那么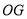 是
是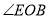 的平分线吗?说明理由.
的平分线吗?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图1),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,现将三角板EFG绕O点顺时针旋转,旋转角
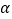 满足条件
满足条件 四边形CHGK是旋转过程中两三角板的重叠部分(如图2).
四边形CHGK是旋转过程中两三角板的重叠部分(如图2).(1)在上述旋转过程中,BH与CK有怎样的数量关系?证明你的结论;
(2)在上述旋转过程中,两个直角三角形的重叠部分面积是否会发生改变?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平整的地面上,用若干个完全相同的棱长为10 cm的小正方体堆成一个几何体.
(1)现已给出这个几何体的俯视图(如图②),请你画出这个几何体的主视图与左视图;
(2)若现在你手头还有一些相同的小正方体,如果保持这个几何体的主视图和俯视图不变.
①在图①所示的几何体中最多可以再添加几个小正方体?
②在图①所示的几何体中最多可以拿走几个小正方体?
③在②的情况下,把这个几何体放置在墙角,如图③所示是此时这个几何体放置的俯视图,若给这个几何体表面喷上红漆,则需要喷漆的面积最少是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线
 上有三点
上有三点 、
、 、
、 ,满足
,满足 ,
,  ,
,  ,点
,点 从点
从点 出发,沿
出发,沿 方向以
方向以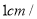 秒的速度匀速运动,点
秒的速度匀速运动,点 从点
从点 出发在线段
出发在线段 上向点
上向点 匀速运动,两点同时出发,当点
匀速运动,两点同时出发,当点 运动到点
运动到点 时,点
时,点 、
、 停止运动.
停止运动.(1)若点
 运动速度为
运动速度为 秒,经过多长时间
秒,经过多长时间 、
、 两点相遇?
两点相遇?(2)当
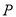 在线段
在线段 上且
上且 时,点
时,点 运动到的位置恰好是线段
运动到的位置恰好是线段 的三等分点,
的三等分点,求点
 的运动速度;
的运动速度;(3)当点
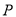 运动到线段
运动到线段 上时,分别取
上时,分别取 和
和 的中点
的中点 、
、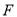 ,求
,求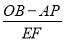 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的七边形ABCDEFG中,∠1、∠2、∠3、∠4 四个角的外角和为180°,∠5 的外角为60°,BP、DP 分别平分∠ABC、∠CDE,则∠BPD 的度数是( )

A. 130° B. 120° C. 110° D. 100°
相关试题

