搜索
【题目】计算或解方程
（1）﹣14+（﹣5）2×（﹣
）+|0.8﹣1|
（2）﹣1.53×0.75+1.53×
+
×1.53
（3）
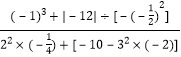
（4）
．
参考答案：
【答案】（1）-
（2）1.53（3）-7（4）x＝﹣7.9
【解析】
（1）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果；
（2）原式先计算开方，再应用乘法分配律计算即可；
（3）原式先计算乘方运算，再计算乘除运算，最后分数化简即可；
（4）原方程去分母、去括号、移项、合并同类项、系数化1即可解答.
（1）原式＝﹣1﹣
+0.2＝﹣
﹣＝﹣；
（2）原式＝1.53×（﹣0.75+
+
）＝1.53；
（3）原式＝
＝﹣7；
（4）方程整理得：
﹣
＝1，
去分母得：70x+70﹣60x+30＝21，
移项合并得：10x＝﹣79，
解得：x＝﹣7.9．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，A（1，0）、点B在y轴上，将三角形OAB沿x轴负方向平移，平移后的图形为三角形DEC，且点C的坐标为（-3，2）．
（1）直接写出点E的坐标；
（2）在四边形ABCD中，点P从点B出发，沿“BC→CD”移动．若点P的速度为每秒1个单位长度，运动时间为t秒，回答下列问题：
①当t等于多少秒时，点P的横坐标与纵坐标互为相反数；
②求点P在运动过程中的坐标，（用含t的式子表示，写出过程）；
③当3秒＜t＜5秒时，设∠CBP=x°，∠PAD=y°，∠BPA=z°，用含x，y的式子表示z.
-
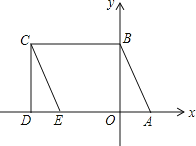
科目： 来源： 题型：
查看答案和解析>>【题目】（感知）如图①，AB∥CD，点E在直线AB与CD之间，连结AE、BE，试说明∠BEE+∠DCE＝∠AEC．下面给出了这道题的解题过程，请完成下面的解题过程，并填空（理由或数学式）：
解：如图①，过点E作EF∥AB
∴∠BAE＝∠1（ ）
∵AB∥CD（ ）
∴CD∥EF（ ）
∴∠2＝∠DCE
∴∠BAE+∠DCE＝∠1+∠2（ ）
∴∠BAE+∠DCE＝∠AEC
（探究）当点E在如图②的位置时，其他条件不变，试说明∠AEC+∠FGC+∠DCE＝360°；
（应用）点E、F、G在直线AB与CD之间，连结AE、EF、FG和CG，其他条件不变，如图③．若∠EFG＝36°，则∠BAE+∠AEF+∠FGC+∠DCG＝ °．
-
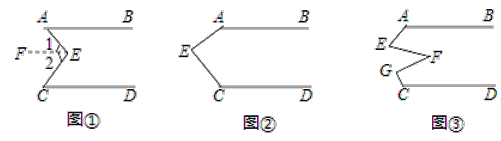
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点
的坐标为
，以 A 为顶点的
的两边始终与 
轴交于 
、
两点（在 左面），且
．（1）如图，连接
，当 
时，试说明：
．
（2）过点
作
轴，垂足为
，当
时，将沿
所在直线翻折，翻折后边
交 
轴于点 
，求点 的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，∠E＝∠F＝90°，∠B＝∠C，AE＝AF．有以下结论：①EM＝FN；②CD＝DN；③∠FAN＝∠EAM；④△ACN≌△ABM．其中正确的有（ ）．
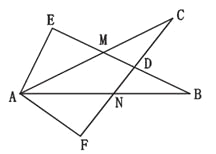
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
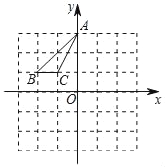
查看答案和解析>>【题目】如图，在平面直角坐标系中，三角形ABC的顶点A、B、C的坐标分别为（0，3）、（﹣2，1）、（﹣1，1），如果将三角形ABC先向右平移2个单位长度，再向下平移2个单位长度，会得到三角形A′B′C′，点A'、B′、C′分别为点A、B、C移动后的对应点．
（1）请直接写出点A′、B'、C′的坐标；
（2）请在图中画出三角形A′B′C′，并直接写出三角形A′B′C′的面积．
-
科目： 来源： 题型：
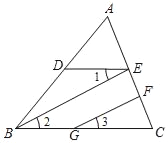
查看答案和解析>>【题目】已知：如图，BE∥GF，∠1＝∠3，∠DBC＝70°，求∠EDB的大小．
阅读下面的解答过程，并填空(理由或数学式)
解：∵BE∥GF(已知)
∴∠2＝∠3( )
∵∠1＝∠3( )
∴∠1＝( )( )
∴DE∥( )( )
∴∠EDB+∠DBC＝180°( )
∴∠EDB＝180°﹣∠DBC(等式性质)
∵∠DBC＝( )(已知)
∴∠EDB＝180°﹣70°＝110°
相关试题
