【题目】如图,在等腰Rt△ABC中,AC=BC=2 ![]() ,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是
,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是 
参考答案:
【答案】π
【解析】解:取AB的中点O、AE的中点E、BC的中点F,连结OC、OP、OM、OE、OF、EF,如图, 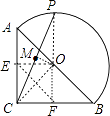
∵在等腰Rt△ABC中,AC=BC=2 ![]() ,
,
∴AB= ![]() BC=4,
BC=4,
∴OC= ![]() AB=2,OP=
AB=2,OP= ![]() AB=2,
AB=2,
∵M为PC的中点,
∴OM⊥PC,
∴∠CMO=90°,
∴点M在以OC为直径的圆上,
点P点在A点时,M点在E点;点P点在B点时,M点在F点,易得四边形CEOF为正方形,EF=OC=2,
∴M点的路径为以EF为直径的半圆,
∴点M运动的路径长= ![]() 2π1=π.
2π1=π.
所以答案是π.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠a与∠β的两边分别平行,∠α比∠β的3倍少24°,则∠β的度数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果以北为正方向,向北走8米记作+8米,那么﹣2米表示( )
A.向北走了2米B.向西走了2米
C.向南走了2米D.向东走了2米
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.

(1)任意闭合其中一个开关,则小灯泡发光的概率等于;
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠F,∠C=∠D, 根据图形填空,并在括号内注明理由.

解:∵∠A=∠F
∴AC∥________(内错角相等,两直线平行)
∴∠1 =∠D(_________________________________)
∵∠C =∠D(已知)
∴∠1=___________(等量代换)
∴BD∥___________(________________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=10,AC=2
 ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
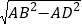 =8,CD=
=8,CD= =2,
=2,此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
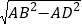 =8,CD=
=8,CD= =2,
=2,此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
相关试题

