搜索
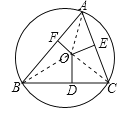
【题目】如图，△ ABC的角A，B，C所对边分别为a，b，c，点O是△ABC的外心，OD⊥BD于D，OE⊥AC于E，OF⊥AB于F，则OD∶OE∶OF为( )
A. a∶b∶c B. 
：
：
C. sinA∶sinB∶sinC D. cosA∶cosB∶cosC
参考答案：
【答案】D
【解析】如图，连接OA、OB、OC，由圆周角定理和等腰三角形三线合一的性质可得∠BOC=2∠BAC=2∠BOD，所以∠BAC=∠BOD；同理样的方法可得∠BOF=∠BCA，∠AOE=∠ABC；设⊙O的半径为R，根据锐角三角函数的定义可得OD=Rcos∠BOD=Rcos∠BAC，OE=Rcos∠AOE=Rcos∠ABC，OF=Rcos∠BOF=Rcos∠ACB，所以OD：OE：OF=cos∠BAC：cos∠ABC：cos∠ACB，故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一只蚂蚁如果沿长方体的表面从A点爬到B’点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.
-
科目： 来源： 题型：
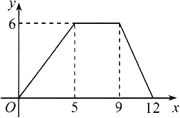
查看答案和解析>>【题目】如图，是一对变量满足的函数关系的图象，有下列3个不同的问题情境：
①小明骑车以400米/分的速度匀速骑了5分，在原地休息了4分，然后以500米/分的速度匀速骑回出发地，设时间为x分，离出发地的距离为y千米；
②有一个容积为6升的开口空桶，小亮以1.2升/分的速度匀速向这个空桶注水，注5分后停止，等4分后，再以2升/分的速度匀速倒空桶中的水，设时间为x分，桶内的水量为y升；
③矩形ABCD中，AB=4，BC=3，动点P从点A出发，依次沿对角线AC、边CD、边DA运动至点A停止，设点P的运动路程为x，当点P与点A不重合时，y=S△ABP；当点P与点A重合时，y=0．
其中，符合图中所示函数关系的问题情境的个数为
A．0 B．1 C．2 D．3
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是（ ）
A. ﹣|﹣2|＝2B. ﹣22＝﹣4C. （﹣2）2＝﹣4D. 33＝9
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=a（x﹣m）2+n与y轴交于点A，它的顶点为点B，点A、B关于原点O的对称点分别为C、D．若A、B、C、D中任何三点都不在一直线上，则称四边形ABCD为抛物线的伴随四边形，直线AB为抛物线的伴随直线．
（1）如图1，求抛物线y=（x﹣2）2+1的伴随直线的解析式．
（2）如图2，若抛物线y=a（x﹣m）2+n（m＞0）的伴随直线是y=x﹣3，伴随四边形的面积为12，求此抛物线的解析式．
（3）如图3，若抛物线y=a（x﹣m）2+n的伴随直线是y=﹣2x+b（b＞0），且伴随四边形ABCD是矩形．
①用含b的代数式表示m、n的值；
②在抛物线的对称轴上是否存在点P，使得△PBD是一个等腰三角形？若存在，请直接写出点P的坐标（用含b的代数式表示）；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若单项式﹣x6y与x3ny是同类项，则n的值是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=60cm，BC=80cm，则△AEF的周长是多少？
相关试题
