【题目】如图,在△ABC中,AB=AC=15,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且tanα=![]() 有以下的结论:① △ADE∽△ACD;② 当CD=9时,△ACD与△DBE全等;③ △BDE为直角三角形时,BD为12或
有以下的结论:① △ADE∽△ACD;② 当CD=9时,△ACD与△DBE全等;③ △BDE为直角三角形时,BD为12或![]() ;④ 0<BE≤
;④ 0<BE≤![]() ,其中正确的结论是___________(填入正确结论的序号)
,其中正确的结论是___________(填入正确结论的序号)

参考答案:
【答案】②③.
【解析】
试题解析:①∵∠ADE=∠B,∠DAE=∠BAD,
∴△ADE∽△ABD;
故①错误;
②作AG⊥BC于G,

∵∠ADE=∠B=α,tan∠α=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴cosα=![]() ,
,
∵AB=AC=15,
∴BG=12,
∴BC=24,
∵CD=9,
∴BD=15,
∴AC=BD.
∵∠ADE+∠BDE=∠C+∠DAC,∠ADE=∠C=α,
∴∠EDB=∠DAC,
在△ACD与△DBE中,
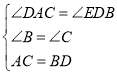 ,
,
∴△ACD≌△BDE(ASA).
故②正确;
③当∠BED=90°时,由①可知:△ADE∽△ABD,
∴∠ADB=∠AED,
∵∠BED=90°,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴∠ADE=∠B=α且tan∠α=![]() ,AB=15,
,AB=15,
∴![]()
∴BD=12.
当∠BDE=90°时,易证△BDE∽△CAD,
∵∠BDE=90°,
∴∠CAD=90°,
∵∠C=α且cosα=![]() ,AC=15,
,AC=15,
∴cosC=![]() ,
,
∴CD=![]() .
.
∵BC=24,
∴BD=24-![]() =
=![]()
即当△DCE为直角三角形时,BD=12或![]() .
.
故③正确;
④易证得△BDE∽△CAD,由②可知BC=24,
设CD=y,BE=x,
∴![]() ,
,
∴![]() ,
,
整理得:y2-24y+144=144-15x,
即(y-12)2=144-15x,
∴0<x≤![]() ,
,
∴0<BE≤![]() .
.
故④错误.
故正确的结论为:②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则下列结论正确的有( )

(1)∠C′EF=32°;(2)∠AEC=148°;
(3)∠BGE=64°; (4)∠BFD=116°.
A.1个
B.2个
C.3个
D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠MAN的度数为 度.

-
科目: 来源: 题型:
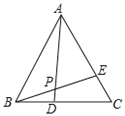
查看答案和解析>>【题目】如图,在等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD=____ _°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(1)x2-4x-5=0; (2)(2-x)2=4-x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】点Q(x, y)在第四象限,且| x | = 3, | y | = 2 , 则点Q的坐标是___________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小丽是同班同学,小明的家距学校2千米远,小丽的家距学校5千米远,设小明家距小丽家x千米远,则x的值应满足( )
A.x=3 B.x=7 C.x=3或x=7 D.3≤x≤7
相关试题

