【题目】如图:AC为一条直线,O是AC上一点, OE、OF分别平分∠AOB和∠BOC.
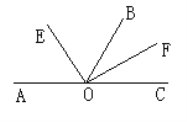
(1)如图:若∠AOB=120°,求∠EOF的大小;
(2)若∠AOB=60°,则∠EOF= _______ °;
(3)任意改变∠AOB的大小,∠EOF的大小会改变吗?
参考答案:
【答案】(1)90°;(2)90°;(3)不变.
【解析】
(1)先由∠AOB=120°,得∠COB=60°,再由OE,OF分别平分∠AOB,∠BOC,得∠EOB=60° ,∠BOF=30°,从而可得∠EOF的大小;
(2)由∠AOB=60°,得∠COB=120°,再由OE,OF分别平分∠AOB,∠BOC,得∠EOB=30° ,∠BOF=60°,从而可得∠EOF的大小;
(3)任意改变∠AOB的大小,先由点O是AC上一点,得出∠AOB+∠BOC=∠AOC=180°,再由OE,OF分别平分∠AOB,∠BOC,根据角平分线定义得出∠BOE=![]() ∠AOB,∠BOF=
∠AOB,∠BOF=![]() ∠BOC,那么∠EOF=∠BOE+∠BOF=
∠BOC,那么∠EOF=∠BOE+∠BOF=![]() ∠AOB+
∠AOB+![]() ∠BOC=
∠BOC=![]() ∠AOC=90°.
∠AOC=90°.
(1)∵∠AOB=120°,∴∠COB=180°-120°=60°
∵OE、OF分别平分∠AOB和∠BOC
∴∠EOB=![]() ∠AOB=60° ,∠BOF=
∠AOB=60° ,∠BOF=![]() ∠BOC=30°
∠BOC=30°
∴∠EOF=∠EOB+∠BOF=60°+30°=90°
(2) ∵∠AOB=60°,∴∠COB=180°-60°=120°
∵OE、OF分别平分∠AOB和∠BOC
∴∠EOB=![]() ∠AOB=30° ,∠BOF=
∠AOB=30° ,∠BOF=![]() ∠BOC=60°
∠BOC=60°
∴∠EOF=∠EOB+∠BOF=30°+60°=90°
(3)不变.
理由是:∵OE平分∠AOB,OF平分∠BOC,
∴∠BOE=![]() ∠AOB,
∠AOB,
∴∠BOF=![]() ∠BOC,
∠BOC,
∴∠EOF=∠BOE+∠BOF=![]() ∠AOB+
∠AOB+![]() ∠BOC=
∠BOC=![]() (∠AOB+∠BOC)=
(∠AOB+∠BOC)=![]() ×180°=90°.
×180°=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)2(3x+4)-5(x+1)=4
(2)6-3(x+
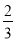 )=
)=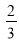
(3)
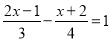
(4)
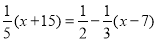
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+4的图像与反比例函数
 (k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.(1)求此反比例函数的表达式;
(2)若点P在x轴上,且
 ,求点P的坐标.
,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装公司招工广告承诺:“熟练工人每月工资至少3800元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资,且加工1件A型服装计酬20元,加工1件B型服装计酬15元”. (工人月工资=底薪+计件工资)在实际工作中发现一名熟练工加工1件A型服装的时间是加工1件B型服装的2倍,且工作5天(即40小时)单独加工B服装的件数比单独加工A服装的件数多20件.
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
-
科目: 来源: 题型:
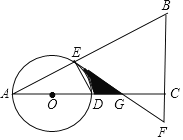
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
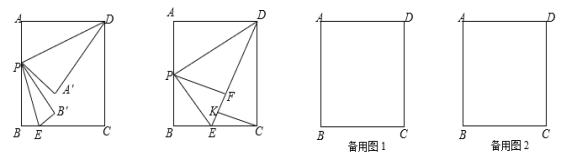
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=6,点P、点E分别是边AB、BC上的动点,连结DP、PE.将△ADP与△BPE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处.
(1) 当点P运动到边AB的中点处时,点A′与点B′重合于点F处,过点C作CK⊥EF于K,求CK的长;
(2) 当点P运动到某一时刻,若P,A',B'三点恰好在同一直线上,且A'B'=4 ,试求此时AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校部分师生要去外地参加夏令营活动,车站提出两种车票价格优惠方案供学校选择:第一种方案是教师按原价付款,学生按原价的75%付款;第二种方案是师生都按原价的80%付款.已知该校有5名教师和x名学生参加此次夏令营活动,车票原价为100元/张.
(1)分别写出两种方案的购票款(列代数式并化简)
(2)如果两种方案的付款相同,那么参加夏令营的学生有多少人?
(3)当参加夏令营的学生人数为
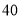 名时,试说明选择哪一种方案购票省钱?
名时,试说明选择哪一种方案购票省钱?
相关试题

