搜索
【题目】在平面直角坐标系中，点（2，1）在第象限．
参考答案：
【答案】一
【解析】解：在平面直角坐标系中，点（2，1）在第一象限， 所以答案是：一．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲乙丙丁四支足球队在全国甲级联赛中进球数分别为：9，9，x ， 7，若这组数据的众数与平均数恰好相等，则这组数据的中位数是（ ）
A.10
B.9
C.8
D.7 -
科目： 来源： 题型：
查看答案和解析>>【题目】公园里有甲、乙两群游客正在做团体游戏，两群游客的年龄如下（单位：岁）：
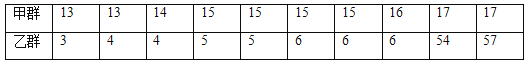
（1）甲群游客的平均年龄是多少？中位数、众数呢？
（2）乙群游客的平均年龄是多少？中位数、众数呢？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（﹣4，﹣1）、B（﹣2，3）、C（2，0），将△ABC先向右平移5个单位，再向上平移3个单位，得到△A1B1C1 ．
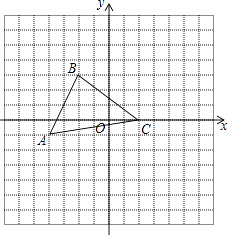
（1）画出△A1B1C1；
（2）写出点A1 ， B1 ， C1的坐标．
（3）求△ABC的面积． -
科目： 来源： 题型：
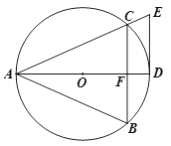
查看答案和解析>>【题目】如图，⊙O为等腰三角形ABC的外接圆，AB=AC，AD是⊙O的直径，切线DE与AC的延长线相交于点E．
（1）求证：DE∥BC；
（2）若DF=n，∠BAC=2α，写出求CE长的思路．
-
科目： 来源： 题型：
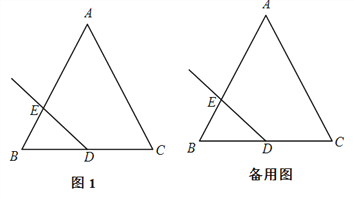
查看答案和解析>>【题目】在△ABC中，AB=AC，∠A=60°，点D是BC边的中点，作射线DE，与边AB交于点E，射线DE绕点D顺时针旋转120°，与直线AC交于点F．
（1）依题意将图1补全；
（2）小华通过观察、实验提出猜想：在点E运动的过程中，始终有DE=DF．小华把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：由点D是BC边的中点，通过构造一边的平行线，利用全等三角形，可证DE=DF；
想法2：利用等边三角形的对称性，作点E关于线段AD的对称点P，由∠BAC与∠EDF互补，可得∠AED与∠AFD互补，由等角对等边，可证DE=DF；
想法3：由等腰三角形三线合一，可得AD是∠BAC的角平分线，由角平分线定理，构造点D到AB，AC的高，利用全等三角形，可证DE=DF…….
请你参考上面的想法，帮助小华证明DE=DF（选一种方法即可）；
（3）在点E运动的过程中，直接写出BE，CF，AB之间的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线
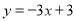与x轴，y轴分别交于A，B两点，点A关于直线
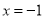的对称点为点C．
（1）求点C的坐标；
（2）若抛物线
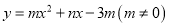经过A，B，C三点，求该抛物线的表达式；（3）若抛物线
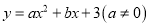经过A，B两点，且顶点在第二象限，抛物线与线段AC有两个公共点，求a的取值范围．
相关试题
