【题目】如图,在平面直角坐标系![]() 中,将抛物线
中,将抛物线![]() 的对称轴绕着点
的对称轴绕着点![]() (0,2)顺时针旋转45°后与该抛物线交于
(0,2)顺时针旋转45°后与该抛物线交于![]() 两点,点
两点,点![]() 是该抛物线上的一点.
是该抛物线上的一点.
(1)求![]() 两点的坐标。
两点的坐标。
(2)如图①,若点![]() 在直线
在直线![]() 的下方,求点
的下方,求点![]() 到直线
到直线![]() 的距离的最大值;
的距离的最大值;
(3)如图②,若点![]() 在
在![]() 轴左侧,且点
轴左侧,且点![]() 是直线
是直线![]() 上一点,当以
上一点,当以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似时,求所有满足条件的
相似时,求所有满足条件的![]() 的值.
的值.
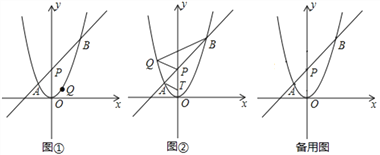
参考答案:
【答案】(1) A(-1,1) B(2,4);(2) ![]() ; (3) t=1或t=0或t=1﹣
; (3) t=1或t=0或t=1﹣![]() 或t=3﹣
或t=3﹣![]() .
.
【解析】分析:(1)根据题意易得点M、P的坐标,利用待定系数法来求直线AB的解析式;(2)如图①,过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,构建等腰直角△QDC,利用二次函数图象上点的坐标特征和二次函数最值的求法进行解答;(3)根据相似三角形的对应角相等推知: △PBQ中必有一个内角为45°;需要分类讨论: ∠PBQ=45°和∠PQB=45°;然后对这两种情况下的△PAT是否是直角三角形分别进行解答.另外,以P、B、Q为顶点的三角形与△PAT 相似也有两种情况: △![]() ∽△PAT、△
∽△PAT、△![]() ∽△PAT.
∽△PAT.
详解:(1)如图①,设直线AB与x轴的交点为M.
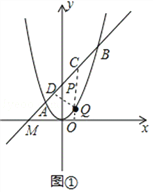
∵∠OPA=45°,∴OM=OP=2,即M(﹣2,0).
设直线AB的解析式为y=kx+b(k≠0),将M(﹣2,0),P(0,2)两点坐标代入,得
![]() ,
,
解得![]() . 故直线AB的解析式为y=x+2;
. 故直线AB的解析式为y=x+2;
联立![]() ,解得
,解得 ![]()
∴ A(-1,1) B(2,4).
(2)如图①,过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,根据条件可知△QDC为等腰直角三角形,则QD=![]() QC.
QC.
设Q(m,m2),则C(m,m+2).
∴QC=m+2﹣m2=﹣(m﹣![]() )2+
)2+![]() ,
,
QD=![]() QC=
QC=![]() [﹣(m﹣
[﹣(m﹣![]() )2+
)2+![]() ].
].
故当m=![]() 时,点Q到直线AB的距离最大,最大值为
时,点Q到直线AB的距离最大,最大值为![]() ;
;
(3)∵∠APT=45°,
∴△PBQ中必有一个内角为45°,由图知,∠BPQ=45°不合题意.
①如图②,若∠PBQ=45°,过点B作x轴的平行线,与抛物线和y轴分别交于点Q′、F.此时满足∠PBQ′=45°.
∵Q′(﹣2,4),F(0,4),
∴此时△BPQ′是等腰直角三角形,由题意知△PAT也是等腰直角三角形.
(i)当∠PTA=90°时,得到:PT=AT=1,此时t=1;
(ii)当∠PAT=90°时,得到:PT=2,此时t=0.
②如图③,若∠PQB=45°,①中是情况之一,答案同上;
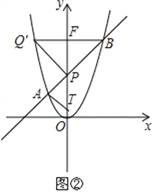
先以点F为圆心,FB为半径作圆,则P、B、Q′都在圆F上,设圆F与y轴左侧的抛物线交于另一点Q″.
则∠PQ″B=∠PQ′B=45°(同弧所对的圆周角相等),即这里的交点Q″也是符合要求.
设Q″(n,n2)(﹣2<n<0),由FQ″=2,得 n2+(4﹣n20=22,即n4﹣7n2+12=0.
解得n2=3或n2=4,而﹣2<n<0,故n=﹣![]() ,即Q″(﹣
,即Q″(﹣![]() ,3).
,3).
可证△PFQ″为等边三角形,所以∠PFQ″=60°,又PQ″=PQ″,
所以∠PBQ″=![]() ∠PFQ″=30°. 则在△PQ″B中,∠PQ″B=45°,∠PBQ″=30°.
∠PFQ″=30°. 则在△PQ″B中,∠PQ″B=45°,∠PBQ″=30°.
(i)若△Q″PB∽△PAT,则过点A作y轴的垂线,垂足为E. 则ET=![]() AE=
AE=![]() ,OE=1,
,OE=1,
所以OT=![]() ﹣1,解得t=1﹣
﹣1,解得t=1﹣![]() ;
;
(ii)若△Q″BP∽△PAT,则过点T作直线AB垂线,垂足为G.
设TG=a,则PG=TG=a,AG=![]() TG=
TG=![]() a,AP=
a,AP=![]() ,
,
∴![]() a+a=
a+a=![]() ,
,
解得PT=![]() a=
a=![]() ﹣1,
﹣1,
∴OT=OP﹣PT=3﹣![]() ,
,
∴t=3﹣![]() .
.
综上所述,所求的t的值为t=1或t=0或t=1﹣![]() 或t=3﹣
或t=3﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,点
 把线段
把线段 分割成
分割成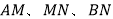 ,若以
,若以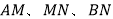 为边的三角形是一个直角三角形,则称
为边的三角形是一个直角三角形,则称 是线段
是线段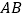 的勾股点。
的勾股点。(1)已知点
 是线段
是线段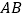 的勾股点,若
的勾股点,若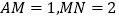 ,求
,求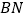 的长。
的长。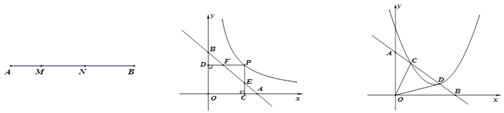
(图1) (图2) (图3)
(2)如图2,点
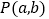 是反比例函数
是反比例函数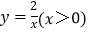 上的动点,直线
上的动点,直线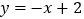 与坐标轴分别交与
与坐标轴分别交与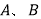 两点,过点
两点,过点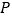 分别向
分别向 轴作垂线,垂足为
轴作垂线,垂足为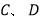 ,且交线段
,且交线段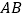 于
于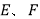 。试证明:
。试证明: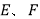 是线段
是线段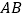 的勾股点。
的勾股点。(3)如图3,已知一次函数
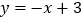 与坐标轴交与
与坐标轴交与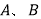 两点,与二次函数
两点,与二次函数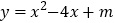 交与
交与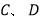 两点,若
两点,若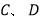 是线段
是线段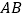 的勾股点,求
的勾股点,求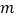 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.

(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,点 C 在以 AB 为直径的⊙O 上,点 D 在 AB 的延长线上,∠BCD =∠A.
(1)求证:CD 为⊙O 的切线;
(2)过点 C 作 CE⊥AB 于点 E.若 CE = 2,cos D =
 ,求 AD 的长.
,求 AD 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小学的时候我们已经学过分数的加减法法则:“同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,转化为同分母分数,再加减.”如:
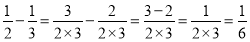 ,反之,这个式子仍然成立,即:
,反之,这个式子仍然成立,即: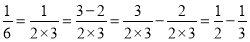 .
.(1)问题发现
观察下列等式:
①
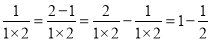 ,
,②
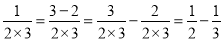 ,
,③
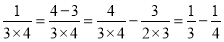 ,…,
,…,猜想并写出第
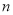 个式子的结果:
个式子的结果: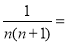 .(直接写出结果,不说明理由)
.(直接写出结果,不说明理由)(2)类比探究
将(1)中的的三个等式左右两边分别相加得:
 ,
,类比该问题的做法,请直接写出下列各式的结果:
①
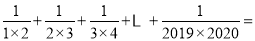 ;
;②
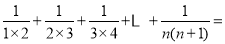 ;
;(3)拓展延伸
计算:
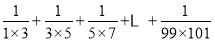 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:阅读下列材料:已知二次三项式2x2+x+a有一个因式是(x+2),求另一个因式以及a 的值
解:设另一个因式是(2x+b),
根据题意,得2x2+x+a=(x+2)(2x+b),
展开,得2x2+x+a =2x2+(b+4)x+2b,
所以
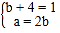 ,解得
,解得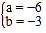 ,
,所以,另一个因式是(2x3),a 的值是6.
请你仿照以上做法解答下题:已知二次三项式3x2 10x m 有一个因式是(x+4),求另一个因式以及m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计表.解答下列问题:
(1) 表中a=__________,b=__________,c=__________
(2) 请补全频数分布直方图;
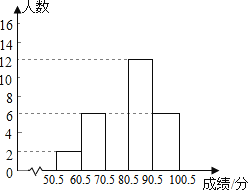
组别
分数段/分
频数/人数
频率
1
50.5~60.5
2
a
2
60.5~70.5
6
0.15
3
70.5~80.5
b
c
4
80.5~90.5
12
0.30
5
90.5~100.5
6
0.15
合计
40
1.00
(3) 该公司共有员工3000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数.
相关试题

