【题目】小学的时候我们已经学过分数的加减法法则:“同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,转化为同分母分数,再加减.”如:![]() ,反之,这个式子仍然成立,即:
,反之,这个式子仍然成立,即:![]() .
.
(1)问题发现
观察下列等式:
①![]() ,
,
②![]() ,
,
③![]() ,…,
,…,
猜想并写出第![]() 个式子的结果:
个式子的结果:![]() .(直接写出结果,不说明理由)
.(直接写出结果,不说明理由)
(2)类比探究
将(1)中的的三个等式左右两边分别相加得:
![]() ,
,
类比该问题的做法,请直接写出下列各式的结果:
①![]() ;
;
②![]() ;
;
(3)拓展延伸
计算:![]() .
.
参考答案:
【答案】(1) ![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)
;(3) ![]() .
.
【解析】
(1)根据题目中的式子可以写出第n个式子的结果;
(2)①根据题目中的式子的特点和(1)中的结果,可以求得所求式子的值;
②根据题目中的式子的特点和(1)中的结果,可以求得所求式子的值;
(3)根据题目中式子的特点,可以求得所求式子的值.
解:(1)由题目中的式子可得,
![]() ,
,
故答案为:![]() ;
;
(2)①![]()
![]()
![]()
![]() ,
,
故答案为:![]() ;
;
②![]()
![]()
![]()
![]() ,
,
故答案为:![]() ;
;
(3)![]()
![]()
![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.

(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,点 C 在以 AB 为直径的⊙O 上,点 D 在 AB 的延长线上,∠BCD =∠A.
(1)求证:CD 为⊙O 的切线;
(2)过点 C 作 CE⊥AB 于点 E.若 CE = 2,cos D =
 ,求 AD 的长.
,求 AD 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
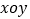 中,将抛物线
中,将抛物线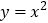 的对称轴绕着点
的对称轴绕着点 (0,2)顺时针旋转45°后与该抛物线交于
(0,2)顺时针旋转45°后与该抛物线交于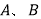 两点,点
两点,点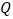 是该抛物线上的一点.
是该抛物线上的一点. (1)求
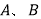 两点的坐标。
两点的坐标。(2)如图①,若点
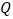 在直线
在直线 的下方,求点
的下方,求点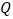 到直线
到直线 的距离的最大值;
的距离的最大值;(3)如图②,若点
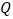 在
在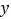 轴左侧,且点
轴左侧,且点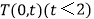 是直线
是直线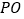 上一点,当以
上一点,当以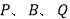 为顶点的三角形与
为顶点的三角形与 相似时,求所有满足条件的
相似时,求所有满足条件的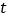 的值.
的值.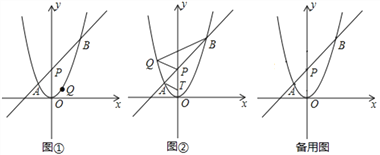
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:阅读下列材料:已知二次三项式2x2+x+a有一个因式是(x+2),求另一个因式以及a 的值
解:设另一个因式是(2x+b),
根据题意,得2x2+x+a=(x+2)(2x+b),
展开,得2x2+x+a =2x2+(b+4)x+2b,
所以
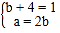 ,解得
,解得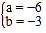 ,
,所以,另一个因式是(2x3),a 的值是6.
请你仿照以上做法解答下题:已知二次三项式3x2 10x m 有一个因式是(x+4),求另一个因式以及m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计表.解答下列问题:
(1) 表中a=__________,b=__________,c=__________
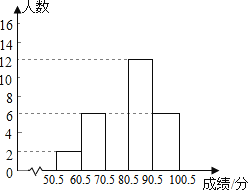
(2) 请补全频数分布直方图;
组别
分数段/分
频数/人数
频率
1
50.5~60.5
2
a
2
60.5~70.5
6
0.15
3
70.5~80.5
b
c
4
80.5~90.5
12
0.30
5
90.5~100.5
6
0.15
合计
40
1.00
(3) 该公司共有员工3000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形 OABC 的 顶 点 A(0,3),C(- 1,0). 将 矩 形 OABC 绕原点顺时针旋转 900,得到矩形 OA’B’C’.解答下列问题:
(1)求出直线 BB’的函数解析式;
(2)直线 BB’与 x 轴交于点 M、与 y 轴交于点N,抛物线 y = ax2+ bx + c 的图象经过点C、M、N,求抛物线的函数解析式.
(3)将△MON 沿直线 MN 翻折,点 O 落在点P 处,请你判断点 P 是否在抛物线上,说明理由.

相关试题

