【题目】已知如图,点 C 在以 AB 为直径的⊙O 上,点 D 在 AB 的延长线上,∠BCD =∠A.
(1)求证:CD 为⊙O 的切线;
(2)过点 C 作 CE⊥AB 于点 E.若 CE = 2,cos D =![]() ,求 AD 的长.
,求 AD 的长.

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)先连接CO,根据AB是⊙O直径,得出∠1+∠OCB=90°,再根据AO=CO,得出∠1=∠A,最后根据∠4=∠A,证出OC⊥CD,即可得出CD为⊙O的切线;
(2)根据OC⊥CD,得出∠3+∠D=90°,再根据CE⊥AB,得出∠3+∠2=90°,从而得出cos∠2=cosD,再在△OCE中根据余弦定义得出CO的值,根据勾股定理求出OE的值,利用sinD=sin∠2,求出OD的值,即可得出AD的长.
试题解析:证明:(1)连接CO.∵AB是⊙O直径,∴∠1+∠OCB=90°.∵AO=CO,∴∠1=∠A.∵∠4=∠A,∴∠4+∠OCB=90°.即∠OCD=90°,∴OC⊥CD.又∵OC是⊙O半径,∴CD为⊙O的切线.
(2)∵OC⊥CD于C,∴∠3+∠D=90°.∵CE⊥AB于E,∴∠3+∠2=90°,∴∠2=∠D,∴cos∠2=cosD.在△OCE中,∠OCD=90°,∴cos∠2=![]() .∵cosD=
.∵cosD=![]() ,CE=2,∴
,CE=2,∴![]() ,∴CO=
,∴CO=![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() ,∴OE=
,∴OE=![]() =
= =
=![]() .∵sinD=sin∠2,
.∵sinD=sin∠2,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,解得:OD=
,解得:OD= ![]() ,AD=OD+OA=
,AD=OD+OA=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D,E,F分别是AB,BC,AC的中点,连接DE,EF,DF,则下列说法不正确的是( )
A. S△DEF=
 S△ABC
S△ABCB. △DEF≌△FAD≌△EDB≌△CFE
C. 四边形ADEF,四边形DBEF,四边形DECF都是平行四边形
D. 四边形ADEF的周长=四边形DBEF的周长=四边形DECF的周长
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,点
 把线段
把线段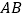 分割成
分割成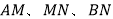 ,若以
,若以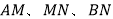 为边的三角形是一个直角三角形,则称
为边的三角形是一个直角三角形,则称 是线段
是线段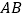 的勾股点。
的勾股点。(1)已知点
 是线段
是线段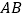 的勾股点,若
的勾股点,若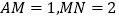 ,求
,求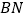 的长。
的长。
(图1) (图2) (图3)
(2)如图2,点
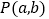 是反比例函数
是反比例函数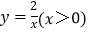 上的动点,直线
上的动点,直线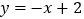 与坐标轴分别交与
与坐标轴分别交与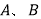 两点,过点
两点,过点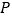 分别向
分别向 轴作垂线,垂足为
轴作垂线,垂足为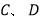 ,且交线段
,且交线段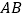 于
于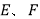 。试证明:
。试证明: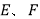 是线段
是线段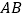 的勾股点。
的勾股点。(3)如图3,已知一次函数
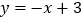 与坐标轴交与
与坐标轴交与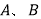 两点,与二次函数
两点,与二次函数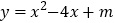 交与
交与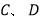 两点,若
两点,若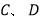 是线段
是线段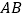 的勾股点,求
的勾股点,求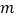 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.

(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
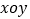 中,将抛物线
中,将抛物线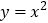 的对称轴绕着点
的对称轴绕着点 (0,2)顺时针旋转45°后与该抛物线交于
(0,2)顺时针旋转45°后与该抛物线交于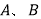 两点,点
两点,点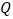 是该抛物线上的一点.
是该抛物线上的一点. (1)求
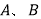 两点的坐标。
两点的坐标。(2)如图①,若点
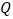 在直线
在直线 的下方,求点
的下方,求点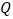 到直线
到直线 的距离的最大值;
的距离的最大值;(3)如图②,若点
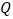 在
在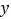 轴左侧,且点
轴左侧,且点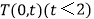 是直线
是直线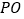 上一点,当以
上一点,当以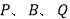 为顶点的三角形与
为顶点的三角形与 相似时,求所有满足条件的
相似时,求所有满足条件的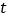 的值.
的值.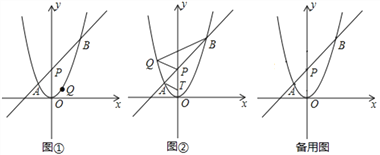
-
科目: 来源: 题型:
查看答案和解析>>【题目】小学的时候我们已经学过分数的加减法法则:“同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,转化为同分母分数,再加减.”如:
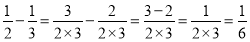 ,反之,这个式子仍然成立,即:
,反之,这个式子仍然成立,即: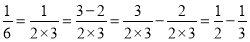 .
.(1)问题发现
观察下列等式:
①
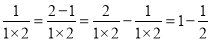 ,
,②
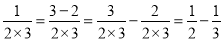 ,
,③
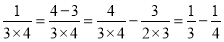 ,…,
,…,猜想并写出第
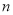 个式子的结果:
个式子的结果: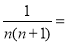 .(直接写出结果,不说明理由)
.(直接写出结果,不说明理由)(2)类比探究
将(1)中的的三个等式左右两边分别相加得:
 ,
,类比该问题的做法,请直接写出下列各式的结果:
①
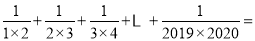 ;
;②
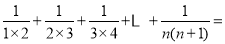 ;
;(3)拓展延伸
计算:
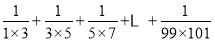 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:阅读下列材料:已知二次三项式2x2+x+a有一个因式是(x+2),求另一个因式以及a 的值
解:设另一个因式是(2x+b),
根据题意,得2x2+x+a=(x+2)(2x+b),
展开,得2x2+x+a =2x2+(b+4)x+2b,
所以
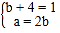 ,解得
,解得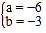 ,
,所以,另一个因式是(2x3),a 的值是6.
请你仿照以上做法解答下题:已知二次三项式3x2 10x m 有一个因式是(x+4),求另一个因式以及m的值.
相关试题

