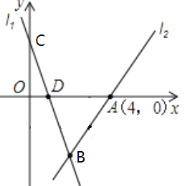
【题目】如图,直线l1:y=﹣3x+3交y轴于C,与x轴交于点D,直线l2经过点A(4,0),且直线l1、l2交于点B(2,m).
(1)求m的值和直线l2的函数表达式;
(2)直线l2在第一象限内的部分上有一点E,且△ADE的面积是△ADB面积的一半,求出点E的坐标,并在x轴上找一点P,使得CP+PE的值最小,求出这个最小值;
(3)若点Q为y轴上一点,且△BDQ为等腰三角形,请直接写出点Q的坐标;
参考答案:
【答案】(1)m=-3,![]() ;(2)E(5,1.5),
;(2)E(5,1.5),![]() ;(3)Q的坐标为
;(3)Q的坐标为![]()
【解析】
(1)将点B(2,m)代入y=﹣3x+3,![]() m=
m=![]() ,即可求出直线l2为
,即可求出直线l2为![]()
(2)先求出D(1,0),![]()
![]() ,设E的坐标为
,设E的坐标为![]() ,根据△ADE的面积是△ADB面积的一半,即可求出E(5,1.5);根据对称性性质作出图像找到C关于x轴的对称点C,,此时CP+PE=C,E,用两点之间距离公式即可求出最小值为C,E的长,
,根据△ADE的面积是△ADB面积的一半,即可求出E(5,1.5);根据对称性性质作出图像找到C关于x轴的对称点C,,此时CP+PE=C,E,用两点之间距离公式即可求出最小值为C,E的长,
(3)分别以B,D为圆心,BD长为半径作弧,可求出与y轴相交的4个交点,再求出BD的中垂线与y轴的交点,即可求出所有满足情况的点.
(1)![]() 点B(2,m)在直线l1:y=﹣3x+3上,
点B(2,m)在直线l1:y=﹣3x+3上,
![]() m=
m=![]()
设直线l2的解析式为y=Kx+b
直线l2经过点A(4,0),点B(2,-3).
![]()
![]()
解得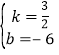
![]() 直线l2的解析式为
直线l2的解析式为![]()
(2)当y=0时,0=-3x+3,x=1
![]() D(1,0)
D(1,0)
![]()
![]() ,
,
设E的坐标为![]() ,
,
则![]()
a=5
![]() E(5,1.5)
E(5,1.5)
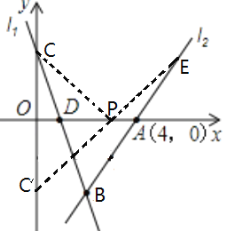
作C关于x轴的对称点C,(0,-3),连接C,E,交x轴于P点,连接CP,如下图,
此时CP+EP有最小值,最小值为C,E的长
![]()
(3)Q的坐标为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理过程:
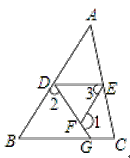
已知:如图,∠1+∠2=180°,∠3=∠B
求证:∠EDG+∠DGC=180°
证明:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°( )
∴∠2= ( )
∴EF∥AB( )
∴∠3= ( )
又∵∠3=∠B(已知)
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG+∠DGC=180°( )
-
科目: 来源: 题型:
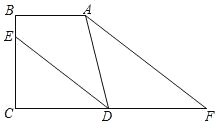
查看答案和解析>>【题目】如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.
(1)求证:∠DAF=∠F;
(2)在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.
-
科目: 来源: 题型:
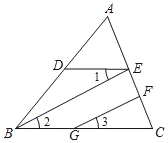
查看答案和解析>>【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
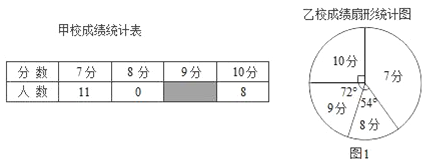
(1)在图1中,“7分”所在扇形的圆心角等于 °.
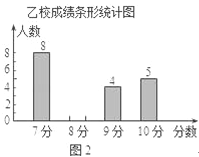
(2)请你将图2的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F.
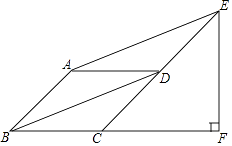
(1)求证:四边形ABCD是菱形;
(2)若∠ABC=45°,BC=2,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?

相关试题

