【题目】完成下列推理过程:
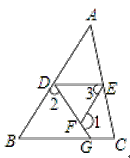
已知:如图,∠1+∠2=180°,∠3=∠B
求证:∠EDG+∠DGC=180°
证明:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°( )
∴∠2= ( )
∴EF∥AB( )
∴∠3= ( )
又∵∠3=∠B(已知)
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG+∠DGC=180°( )
参考答案:
【答案】邻补角定义;∠DFE,同角的补角相等;内错角相等,两直线平行;∠ADE,两直线平行,内错角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补
【解析】
依据∠1+∠2=180°,∠1+∠DFE=180°,即可得到∠2=∠DFE,由内错角相等,两直线平行证明EF∥AB,则∠3=∠ADE,再根据∠3=∠B,由同位角相等,两直线平行证明DE∥BC,故可根据两直线平行,同旁内角互补,即可得出结论.
∵∠1+∠2=180°(已知)
∠1+∠DFE=180°(邻补角定义)
∴∠2=∠DFE(同角的补角相等)
∴EF∥AB(内错角相等,两直线平行)
∴∠3=∠ADE(两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴∠B=∠ADE(等量代换)
∴DE∥BC(同位角相等,两直线平行)
∴∠EDG+∠DGC=180°(两直线平行,同旁内角互补)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy,直线y=x﹣1与y轴交于点A,与双曲线y=
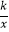 交于点B(m,2).
交于点B(m,2).
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若△ABC的面积为6,求直线CD的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位数,若十位上的数字是百位数字与个位数字的和,我们称这个三位数叫“圣诞数”,并且把这个“圣诞数”的前两位组成的两位数记为m,后两位组成的两位数记为n,并规定d=
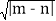 。如一个三位数385,
。如一个三位数385, 3+5=8,
3+5=8, 385是“圣诞数”,且m=38,n=85,则d=
385是“圣诞数”,且m=38,n=85,则d=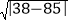 =
=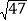 .
.(1)写出最小的“圣诞数”;
(2)求证:任意一个“圣诞数”是11的倍数;
(3)求出所有能被8整除的“圣诞数”,并直接写出这些“圣诞数”中d的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.

-
科目: 来源: 题型:
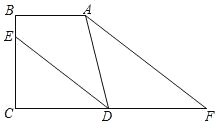
查看答案和解析>>【题目】如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.
(1)求证:∠DAF=∠F;
(2)在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.
-
科目: 来源: 题型:
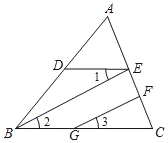
查看答案和解析>>【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
-
科目: 来源: 题型:
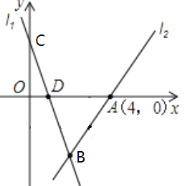
查看答案和解析>>【题目】如图,直线l1:y=﹣3x+3交y轴于C,与x轴交于点D,直线l2经过点A(4,0),且直线l1、l2交于点B(2,m).
(1)求m的值和直线l2的函数表达式;
(2)直线l2在第一象限内的部分上有一点E,且△ADE的面积是△ADB面积的一半,求出点E的坐标,并在x轴上找一点P,使得CP+PE的值最小,求出这个最小值;
(3)若点Q为y轴上一点,且△BDQ为等腰三角形,请直接写出点Q的坐标;
相关试题

