【题目】如图,在平面直角坐标系中,△ABC的点坐标分别为A(2,3),B(1,1),C(2,1).
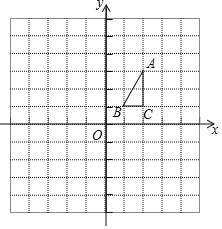
(1)画出△ABC关于x轴对称的△A1B1C1,并写出A1,B1,C1的坐标;
(2)直按写出△ABC关于直线m(直线m上各点的横坐标都为﹣1)对称的△A2B2C2的坐标:A2 ,B2 ,C2 .
参考答案:
【答案】(1)图见解析,A1(2,﹣3),B1(1,﹣1),C1(2,﹣1);(2)A2(﹣4,3),B2(﹣3,1),C2(﹣4,1);
【解析】
(1)依据轴对称的性质,即可得到△ABC关于x轴对称的△A1B1C1,进而得出A1,B1,C1的坐标;
(2)依据轴对称的性质,即可得到△ABC关于直线m对称的△A2B2C2的坐标.
解:(1)如图所示,△A1B1C1即为所求;A1(2,﹣3),B1(1,﹣1),C1(2,﹣1);
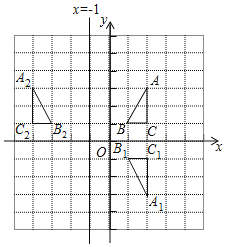
(2)直线m上各点的横坐标都为﹣1,即直线m=-1,如图所示,A2 (﹣4,3),B2 (﹣3,1),C2(﹣4,1).
故答案为:(﹣4,3),(﹣3,1),(﹣4,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图1,在ABCD中,点E是AB中点,连接DE并延长,交CB的延长线于点F.
(1)求证:△ADE≌△BFE;
(2)如图2,点G是边BC上任意一点(点G不与点B、C重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.
①求证:HC=2AK;
②当点G是边BC中点时,恰有HD=nHK(n为正整数),求n的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
如图1所示,直线y=x+c与x轴交于点A(﹣4,0),与y轴交于点C,抛物线y=﹣x2+bx+c经过点A,C.
(1)求抛物线的解析式
(2)点E在抛物线的对称轴上,求CE+OE的最小值;
(3)如图2所示,M是线段OA的上一个动点,过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N
①若以C,P,N为顶点的三角形与△APM相似,则△CPN的面积为 ;
②若点P恰好是线段MN的中点,点F是直线AC上一个动点,在坐标平面内是否存在点D,使以点D,F,P,M为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣
 ,
, )
)
-
科目: 来源: 题型:
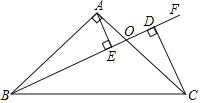
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,过C作CD垂直射线BF于点D,射线BF交AC于点O,过A作AE⊥BO于点E,若BD=13,AE=4,则CD=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD中,∠BAD=80°,C为BD延长线上一点,∠BAC=130°,∠ABD的角平分线与AC交于点E,连接DE.

(1)求证:点E到DA、DC的距离相等;
(2)求∠BED的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 图象的顶点为
图象的顶点为 ,其图象与
,其图象与 轴的交点
轴的交点 、
、 的横坐标分别为
的横坐标分别为 ,
, .与
.与 轴负半轴交于点
轴负半轴交于点 ,在下面五个结论中:
,在下面五个结论中:①
 ;②
;② ;③
;③ ;④只有当
;④只有当 时,
时, 是等腰直角三角形;⑤使
是等腰直角三角形;⑤使 为等腰三角形的
为等腰三角形的 值可以有四个.
值可以有四个.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形
 置于平面直角坐标系中,点
置于平面直角坐标系中,点 的坐标为
的坐标为 ,点
,点 在
在 轴上,点
轴上,点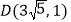 在
在 上,将矩形
上,将矩形 沿
沿 折叠压平,使点
折叠压平,使点 落在坐标平面内,设点
落在坐标平面内,设点 的对应点为点
的对应点为点 .若抛物线
.若抛物线 (
( 且
且 为常数)的顶点落在
为常数)的顶点落在 的内部,则
的内部,则 的取值范围是( )
的取值范围是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

