【题目】如图,将矩形![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 上,将矩形
上,将矩形![]() 沿
沿![]() 折叠压平,使点
折叠压平,使点![]() 落在坐标平面内,设点
落在坐标平面内,设点![]() 的对应点为点
的对应点为点![]() .若抛物线
.若抛物线![]() (
(![]() 且
且![]() 为常数)的顶点落在
为常数)的顶点落在![]() 的内部,则
的内部,则![]() 的取值范围是( )
的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
利用对折的性质,得到线段的关系,用勾股定理建立方程,最后用相似△AFG∽△ABD得到比例式![]() ,计算出点G,H的纵坐标即可.
,计算出点G,H的纵坐标即可.
如图,
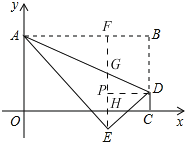
过点E作EF⊥AB于F,EF分别与AD、OC交于点G、H,
过点D作DP⊥EF于点P,
则EP=PH+EH=DC+EH=1+EH,
在Rt△PDE中,由勾股定理可得,
DP2=DE2-PE2=9+(1+EH)2,
∴BF2=DP2=9+(1+EH)2,
在Rt△AEF中,AF=AB-BF=3![]() -
-![]() ,EF=4+EH,AE=4,
,EF=4+EH,AE=4,
∵AF2+EF2=AE2,
即:(3![]() -
-![]() )2+(4+EH)2=16,
)2+(4+EH)2=16,
解得EH=1,
∴AB=3![]() ,AF=2
,AF=2![]() ,E(2
,E(2![]() ,-1).
,-1).
∵∠AFG=∠ABD=90°,∠FAG=∠BAD,
∴△AFG∽△ABD.
∴![]() ,
,
即:![]() ,
,
∴FG=2.
∴EG=EF-FG=3.
∴点G的纵坐标为2.
∵y=ax2-4![]() ax+10=a(x-2
ax+10=a(x-2![]() )2+(10-20a),
)2+(10-20a),
∴此抛物线y=ax2-4![]() ax+10的顶点必在直线x=2
ax+10的顶点必在直线x=2![]() 上.
上.
又∵抛物线的顶点落在△ADE的内部,
∴此抛物线的顶点必在EG上.
∴-1<10-20a<2,
∴![]() .
.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的点坐标分别为A(2,3),B(1,1),C(2,1).
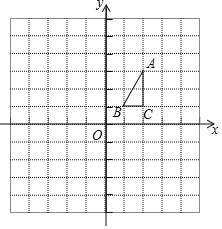
(1)画出△ABC关于x轴对称的△A1B1C1,并写出A1,B1,C1的坐标;
(2)直按写出△ABC关于直线m(直线m上各点的横坐标都为﹣1)对称的△A2B2C2的坐标:A2 ,B2 ,C2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD中,∠BAD=80°,C为BD延长线上一点,∠BAC=130°,∠ABD的角平分线与AC交于点E,连接DE.

(1)求证:点E到DA、DC的距离相等;
(2)求∠BED的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 图象的顶点为
图象的顶点为 ,其图象与
,其图象与 轴的交点
轴的交点 、
、 的横坐标分别为
的横坐标分别为 ,
, .与
.与 轴负半轴交于点
轴负半轴交于点 ,在下面五个结论中:
,在下面五个结论中:①
 ;②
;② ;③
;③ ;④只有当
;④只有当 时,
时, 是等腰直角三角形;⑤使
是等腰直角三角形;⑤使 为等腰三角形的
为等腰三角形的 值可以有四个.
值可以有四个.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】点
 ,
, 的坐标分别为
的坐标分别为 和
和 ,抛物线
,抛物线 的顶点在线段
的顶点在线段 上运动时,形状保持不变,且与
上运动时,形状保持不变,且与 轴交于
轴交于 ,
, 两点(
两点( 在
在 的左侧),给出下列结论:①
的左侧),给出下列结论:① ;②当
;②当 时,
时, 随
随 的增大而增大;③若点
的增大而增大;③若点 的横坐标最大值为
的横坐标最大值为 ,则点
,则点 的横坐标最小值为
的横坐标最小值为 ;④当四边形
;④当四边形 为平行四边形时,
为平行四边形时, .其中正确的是( )
.其中正确的是( )A. ②④ B. ②③ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:

①在岸边确定一点C,使C与A,B在同一直线上;
②在AC的垂直方向画线段CD,取其中点O;
③画DF⊥CD使F、O、A在同一直线上;
④在线段DF上找一点E,使E与O、B共线.
他说测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AP是△ABC的外角平分线,连结PB、PC.
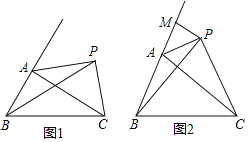
(1)如图1①若BP平分∠ABC,且∠ACB=28°,求∠APB的度数.
②若P与A不重合,请判断AB+AC与PB+PC的大小关系,并证明你的结论.
(2)如图2,若过点P作PM⊥BA,交BA的延长线于M点,且∠BPC=∠BAC,求:
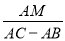 的值.
的值.
相关试题

