【题目】已知,如图1,在ABCD中,点E是AB中点,连接DE并延长,交CB的延长线于点F.
(1)求证:△ADE≌△BFE;
(2)如图2,点G是边BC上任意一点(点G不与点B、C重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.
①求证:HC=2AK;
②当点G是边BC中点时,恰有HD=nHK(n为正整数),求n的值.

参考答案:
【答案】(1)详见解析;(2)详见解析;(3)n=4.
【解析】
(1)根据平行四边形的性质得到AD∥BC,得到∠ADE=∠BFE,∠A=∠FBE,利用AAS定理证明即可;
(2)作BN∥HC交EF于N,根据全等三角形的性质、三角形中位线定理证明;
(3)作GM∥DF交HC于M,分别证明△CMG∽△CHF、△AHD∽△GHF、△AHK∽△HGM,根据相似三角形的性质计算即可.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠BFE,∠A=∠FBE,
在△ADE和△BFE中,
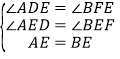
∴△ADE≌△BFE;
(2)如图2,作BN∥HC交EF于N,

∵△ADE≌△BFE,
∴BF=AD=BC,
∴BN=![]() HC,
HC,
由(1)的方法可知,△AEK≌△BFN,
∴AK=BN,
∴HC=2AK;
(3)如图3,作GM∥DF交HC于M,

∵点G是边BC中点,
∴CG=![]() CF,
CF,
∵GM∥DF,
∴△CMG∽△CHF,
∴![]() ,
,
∵AD∥FC,
∴△AHD∽△GHF,
∴![]() ,
,
∴![]() ,
,
∵AK∥HC,GM∥DF,
∴△AHK∽△HGM,
∴![]() ,
,
∴![]() ,即HD=4HK,
,即HD=4HK,
∴n=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:
 ≈2.449,结果保留整数)
≈2.449,结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角三角形ABC中,O为三条边的垂直平分线的交点,I为三个角的平分线的交点,若∠BOC的度为x,∠BIC的度数为y,则x、y之间的数量关系是( )
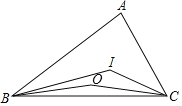
A.x+y=90°B.x﹣2y=90°C.x+180°=2yD.4y﹣x=360°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC的平分线与∠ACD的平分线交于点A
 ,∠A
,∠A BC的平分线与∠A
BC的平分线与∠A CD的平分线交于点A
CD的平分线交于点A ,以此类推,∠A
,以此类推,∠A BC的平分线与∠A
BC的平分线与∠A CD的平分线交于点A
CD的平分线交于点A ,则∠A
,则∠A 的大小是___
的大小是___
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
如图1所示,直线y=x+c与x轴交于点A(﹣4,0),与y轴交于点C,抛物线y=﹣x2+bx+c经过点A,C.
(1)求抛物线的解析式
(2)点E在抛物线的对称轴上,求CE+OE的最小值;
(3)如图2所示,M是线段OA的上一个动点,过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N
①若以C,P,N为顶点的三角形与△APM相似,则△CPN的面积为 ;
②若点P恰好是线段MN的中点,点F是直线AC上一个动点,在坐标平面内是否存在点D,使以点D,F,P,M为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣
 ,
, )
)
-
科目: 来源: 题型:
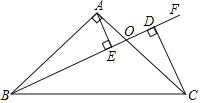
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,过C作CD垂直射线BF于点D,射线BF交AC于点O,过A作AE⊥BO于点E,若BD=13,AE=4,则CD=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的点坐标分别为A(2,3),B(1,1),C(2,1).
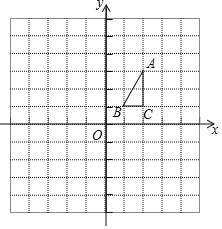
(1)画出△ABC关于x轴对称的△A1B1C1,并写出A1,B1,C1的坐标;
(2)直按写出△ABC关于直线m(直线m上各点的横坐标都为﹣1)对称的△A2B2C2的坐标:A2 ,B2 ,C2 .
相关试题

