Question

【题目】问题情境：如图1，AB∥CD， ,．求度数．

小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得 _______．

问题迁移：如图3，AD∥BC，点P在射线OM上运动， ， ．

（1）当点P在A、B两点之间运动时， 、、之间有何数量关系？请说明理由.

（2）如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出、、之间的数量关系．

Answer 1

【答案】；

（1），理由见解析；

（2）当点P在B、O两点之间时， ；

当点P在射线AM上时， .

【解析】试题分析：（1）过P作PE∥AB，通过平行线性质求∠APC即可；（2）过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案；（3）画出图形，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案．

试题解析：(1)过点P作PE∥AB，

∵AB∥CD，

∴PE∥AB∥CD，

∴∠A+∠APE=180°,∠C+∠CPE=180°，

∵∠PAB=130°,∠PCD=120°，

∴∠APE=50°,∠CPE=60°，

∴∠APC=∠APE+∠CPE=110°.

故答案为110°.

（1）过P作PQ∥AD.

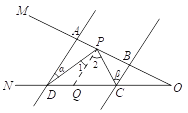
∵AD∥BC，

∴AD∥PQ ，

PQ∥BC

∵PQ∥AD，

∴

同理，

∴

（2）(3)当P在BA延长线时，

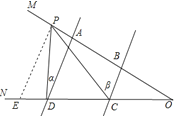
∠CPD=∠β∠α；

当P在AB延长线时，

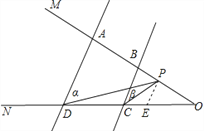
∠CPD=∠α∠β.