搜索
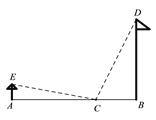
【题目】如图，小明所在学校的旗杆BD高约为13米，距离旗杆20米处刚好有一棵高约为3米的香樟树AE．活动课上，小明有意在旗杆与香樟树之间的连线上来回踱步，发现有一个位置到旗杆顶部与树顶的距离相等．请你求出该位置与旗杆之间的距离.
参考答案：
【答案】该位置与旗杆之间的距离为6米.
【解析】试题分析：
设这个点为点C，连接EC、DC，则由题意可知EC=DC，再设AC= 
米，则BC=（20- 
）米，在两个直角三角形中，由勾股定理分别表达出CE2和CD2，就可列出方程解得
的值，从而就可求出该位置与旗杆之间的距离.
试题解析：
根据题意可得：AE＝3m，AB＝20m，BD＝13m.
如图，设该位置为点C，且AC＝
m.
由AC＝
m得：BC＝(20－
)m.
由题意得：CE＝CD，则CE2＝CD2.
∴
，解得： 
＝14.
∴ CB＝20－
＝6.
由0＜14＜20可知，该位置是存在的.
答：该位置与旗杆之间的距离为6米.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在学习概率的课堂上，老师提出问题：只有一张电影票，小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影，请你设计一个对小明和小刚都公平的方案．
甲同学的方案：将红桃2、3、4、5四张牌背面向上，小明先抽一张，小刚从剩下的三张牌中抽一张，若两张牌上的数字之和是奇数，则小明看电影，否则小刚看电影．
（1）甲同学的方案公平吗？请用列表或画树状图的方法说明；
（2）乙同学将甲的方案修改为只用红桃2、3、4三张牌，抽取方式及规则不变，乙的方案公平吗？（只回答，不说明理由）
-
科目： 来源： 题型：
查看答案和解析>>【题目】若代数式2x2+3y+7的值为8，那么代数式6x2+9y+8的值为（ ）
A.1
B.11
C.15
D.23 -
科目： 来源： 题型：
查看答案和解析>>【题目】为确保信息安全，信息需加密传输，发送方由明文→密文（加密）；接收方由密文→明文（解密）．已知加密规则为：明文a，b，c，d对应的密文为a+b，b+c，c+d，d+2a．例如：明文1，2，3，4对应的密文为3，5，7，6．当接收方收到密文8，11，15，15时，则解密得到的明文应为
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+2（a≠0）与x轴交于A（4，0）、B（﹣1，0）两点，与y轴交于点C．
（1）求抛物线的解析式，并写出其对称轴；
（2）把（1）中所求出的抛物线记为C1，将C1向右平移m个单位得到抛物线C2，C1与C2的在第一象限交点为M，过点M作MG⊥x轴于点G，交线段AC于点H，连接CM，当△CMH为等腰三角形时，求抛物线向右平移的距离m和此时点M的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】2015年5月18日华中旅游博览会在汉召开．开幕式上用到甲、乙、丙三种造型的花束，甲种花束由3朵红花、2朵黄花和1朵紫花搭配而成，乙种花束由2朵红花和2朵黄花搭配而成，丙种花束由2朵红花、1朵黄花和1朵紫花搭配而成．这些花束一共用了580朵红花，150朵紫花，则黄花一共用了 朵．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为确保信息安全，信息需加密传输，发送方由明文→密文（加密）；接收方由密文→明文（解密）．已知加密规则为：明文a，b，c，d对应的密文为a+b，b+c，c+d，d+2a．例如：明文1，2，3，4对应的密文为3，5，7，6．当接收方收到密文8，11，15，15时，则解密得到的明文应为
相关试题
