Question

【题目】如图，抛物线y=ax2+bx+2（a≠0）与x轴交于A（4，0）、B（﹣1，0）两点，与y轴交于点C．

（1）求抛物线的解析式，并写出其对称轴；

（2）把（1）中所求出的抛物线记为C1，将C1向右平移m个单位得到抛物线C2，C1与C2的在第一象限交点为M，过点M作MG⊥x轴于点G，交线段AC于点H，连接CM，当△CMH为等腰三角形时，求抛物线向右平移的距离m和此时点M的坐标．

Answer 1

【答案】(1)、y=﹣x2+x+2，对称轴是：直线x=；(2)、m=1，M（2，3）.

【解析】

试题分析：(1)、利用交点式求二次函数的解析式，并配方求对称轴；(2)、先求直线AC的解析式，根据各自的解析式设出M（x，﹣x2++2），H（x，﹣x+2），由图得△CMH为等腰三角形时，CM=CH，则有GH+GM=4，列式计算求出M的坐标，把M的坐标代入平移后的解析式可并得出m的值．

试题解析：(1)、当x=0时，y=ax2+bx+2=2， ∴抛物线经过（0，2），

∵抛物线y=ax2+bx+2（a≠0）与x轴交于A（4，0）、B（﹣1，0）两点，

设抛物线的解析式为：y=a（x﹣4）（x+1）， 把（0，2）代入得：2=a（0﹣4）（0+1）， a=﹣，

∴y=﹣（x﹣4）（x+1）=﹣x2++2=﹣（x﹣）2+，

∴抛物线的解析式为：y=﹣x2++2，对称轴是：直线x=；

(2)、设直线AC的解析式为：y=kx+b， 把A（4，0）、C（0，2）代入得：，解得：，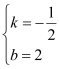

∴直线AC的解析式为：y=﹣x+2， 设M（x，﹣ x2++2），H（x，﹣ x+2），

∵△CMH为等腰三角形， ∴CM=CH， ∴C是MH垂直平分线上的点， ∴GH+GM=4，

则﹣x2++2+（﹣x+2）=4， 解得：x1=0（舍），x2=2， ∴M（2，3），

设平移后的抛物线的解析式为：y=﹣（x﹣﹣m）2+， 把M（2，3）代入得：m=1．