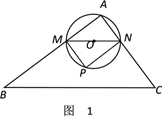
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
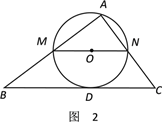
(2)当x为何值时,⊙O与直线BC相切?
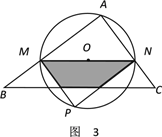
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
参考答案:
【答案】(1)![]() .(0<x<4)(2)x=
.(0<x<4)(2)x=![]() 时,⊙O与直线BC相切;(3)y=-
时,⊙O与直线BC相切;(3)y=-![]() x2+6x-6,当x=
x2+6x-6,当x=![]() 时,y值最大,最大值是2.
时,y值最大,最大值是2.
【解析】试题分析:(1)由于三角形PMN和AMN的面积相当,那么可通过求三角形AMN的面积来得出三角形PMN的面积,求三角形AMN的面积可根据三角形AMN和ABC相似,根据相似比的平方等于面积比来得出三角形AMN的面积;
(2)当圆O与BC相切时,O到BC的距离就是MN的一半,那么关键是求出MN的表达式,可根据三角形AMN和三角形ABC相似,得出MN的表达式,也就求出了O到BC的距离的表达式,如果过M作MQ⊥BC于Q,那么MQ就是O到BC的距离,然后在直角三角形BMQ中,用∠B的正弦函数以及BM的表达式表示出MQ,然后让这两表示MQ的含x的表达式相等,即可求出x的值;
(3)要求重合部分的面积首先看P点在三角形ABC内部还是外面,因此可先得出这两种情况的分界线即当P落到BC上时,x的取值,那么P落点BC上时,MN就是三角形ABC的中位线,此时AM=2,因此可分两种情况进行讨论:
①当0<x≤2时,此时重合部分的面积就是三角形PMN的面积,三角形PMN的面积(1)中已经求出,即可的x,y的函数关系式.②当2<x<4时,如果设PM,PN交BC于E,F,那么重合部分就是四边形MEFN,可通过三角形PMN的面积-三角形PEF的面积来求重合部分的面积.不难得出PN=AM=x,而四边形BMNF又是个平行四边形,可得出FN=BM,也就有了FN的表达式,就可以求出PF的表达式,然后参照(1)的方法可求出三角形PEF的面积,即可求出四边形MEFN的面积,也就得出了y,x的函数关系式.然后根据两种情况得出的函数的性质,以及对应的自变量的取值范围求出y的最大值即可.
试题解析:(1)∵MN∥BC,
∴∠AMN=∠B,∠ANM=∠C.
∴△AMN∽△ABC.
∴![]() ,
,
即![]() ;
;
∴AN=![]() x;
x;
∴S=S△MNP=S△AMN=![]() .(0<x<4)
.(0<x<4)
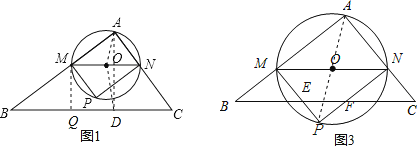
(2)如图2,设直线BC与⊙O相切于点D,连接AO,OD,则AO=OD=![]() MN.
MN.
在Rt△ABC中,BC=![]() =5;
=5;
由(1)知△AMN∽△ABC,
∴![]() ,
,
即![]() ,
,
∴MN= ![]()
∴OD= ![]() ,
,
过M点作MQ⊥BC于Q,则MQ=OD= ![]() ,
,
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴△BMQ∽△BCA,
∴![]() ,
,
∴BM= 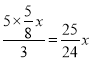 ,AB=BM+MA=
,AB=BM+MA=![]()
∴x=![]() ,
,
∴当x=![]() 时,⊙O与直线BC相切;
时,⊙O与直线BC相切;
(3)随点M的运动,当P点落在直线BC上时,连接AP,则O点为AP的中点.
∵MN∥BC,
∴∠AMN=∠B,∠AOM=∠APB,
∴△AMO∽△ABP,
∴![]() ,
,
∵AM=MB=2,
故以下分两种情况讨论:
①当0<x≤2时,y=S△PMN=![]() x2,
x2,
∴当x=2时,y最大=![]() ×4=
×4=![]() ,
,
②当2<x<4时,设PM,PN分别交BC于E,F,
∵四边形AMPN是矩形,
∴PN∥AM,PN=AM=x,
又∵MN∥BC,
∴四边形MBFN是平行四边形;
∴FN=BM=4-x,
∴PF=x-(4-x)=2x-4,
又∵△PEF∽△ACB,
∴(![]() )2=
)2=![]() ,
,
∴S△PEF=![]() (x-2)2;
(x-2)2;
y=S△MNP-S△PEF=![]() x2-
x2-![]() (x-2)2=-
(x-2)2=-![]() x2+6x-6,
x2+6x-6,
当2<x<4时,y=-![]() x2+6x-6=-
x2+6x-6=-![]() (x-
(x-![]() )2+2,
)2+2,
∴当x=![]() 时,满足2<x<4,y最大=2.
时,满足2<x<4,y最大=2.
综上所述,当x=![]() 时,y值最大,最大值是2.
时,y值最大,最大值是2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米。大家根据所学知识很快计算出了铁塔高AM。亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程。(数据
 ≈1.41,
≈1.41,  ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)
-
科目: 来源: 题型:
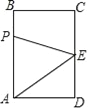
查看答案和解析>>【题目】如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A﹣B﹣C﹣E运动,最终到达点E.若点P运动的时间为x秒,则当x=__时,△APE的面积等于5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①
 ;②
;②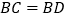 ;③
;③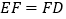 ;④
;④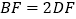 .其中结论一定正确的序号数是( )
.其中结论一定正确的序号数是( )
A. ①② B. ①③ C. ③④ D ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣
 )2=0.
)2=0.(2)先化简,再求值:﹣(3x2﹣4xy)﹣
 [x2﹣2(4x﹣4xy)],其中x=﹣2.
[x2﹣2(4x﹣4xy)],其中x=﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是( )
A.20cm2
B.20πcm2
C.10πcm2
D.5πcm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选一个,并选择你认为适当的方法解这个方程.
①x2﹣4x﹣1=0
②x(2x+1)=8x﹣3
③x2+3x+1=0
④x2﹣9=4(x﹣3)
我选择第个方程.
相关试题

