【题目】已知:如图,ABCD中,E、F分别是AD,BC的中点.求证: 
(1)△AFB≌△CED;
(2)四边形AECF是平行四边形.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,∠B=∠D,AD=BC,
∵E、F分别是AD,BC的中点,
∴AE=DE=FC=BF,
在△AFB和△CED中,
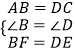 ,
,
∴△AFB≌△CED(SAS)
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵AE=BF,
∴四边形AECF是平行四边形
【解析】(1)利用平行四边形的性质结合全等三角形的判定方法得出即可;(2)利用一组对边平行且相等的四边形是平行四边形进而得出即可.
【考点精析】解答此题的关键在于理解平行四边形的判定与性质的相关知识,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数. 解:因为∠1=∠2=80°(已知),
所以AB∥CD()
所以∠BGF+∠3=180°()
因为∠2+∠EFD=180°(邻补角的性质).
所以∠EFD= . (等式性质).
因为FG平分∠EFD(已知).
所以∠3=∠EFD(角平分线的性质).
所以∠3= . (等式性质).
所以∠BGF= . (等式性质).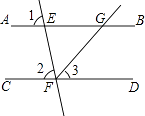
-
科目: 来源: 题型:
查看答案和解析>>【题目】“同旁内角互补”的逆命题是_____________________,它是_____命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD 中,∠A∶∠B∶∠C∶∠D 的值可能是( )
A. 2∶5∶2∶5 B. 3∶4∶4∶5 C. 4∶4∶3∶2 D. 2∶3∶5∶6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3a2=a6
B.a12÷a3=a4
C.a3+b3=(a+b)3
D.(a3)2=a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,AD=3 cm,AB=2 cm,则ABCD的周长等于( )
A. 10 cm B. 6 cm C. 5 cm D. 4 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )

A.
 B.
B.  C.
C.  D.
D. 
相关试题

