【题目】如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数. 解:因为∠1=∠2=80°(已知),
所以AB∥CD()
所以∠BGF+∠3=180°()
因为∠2+∠EFD=180°(邻补角的性质).
所以∠EFD= . (等式性质).
因为FG平分∠EFD(已知).
所以∠3=∠EFD(角平分线的性质).
所以∠3= . (等式性质).
所以∠BGF= . (等式性质).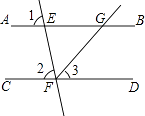
参考答案:
【答案】同位角相等,两直线平行;两直线平行,同旁内角互补;100°;![]() ;50°;130°
;50°;130°
【解析】解:因为∠1=∠2=80°(已知), 所以AB∥CD(同位角相等,两直线平行),
所以∠BGF+∠3=180°(两直线平行,同旁内角互补).
因为∠2+∠EFD=180°(邻补角的性质).
所以∠EFD=100°.(等式性质).
因为FG平分∠EFD(已知).
所以∠3= ![]() ∠EFD(角平分线的性质).
∠EFD(角平分线的性质).
所以∠3=50°.(等式性质).
所以∠BGF=130°.(等式性质).
所以答案是:同位角相等,两直线平行;两直线平行,同旁内角互补;100°; ![]() ;50°;130°.
;50°;130°.
【考点精析】本题主要考查了角的平分线和对顶角和邻补角的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正n边形的一个内角比一个外角大100°,则n为( )
A. 7B. 8C. 9D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=6,AC=8,BC=10,则该三角形为( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】水位上升30cm记作+30cm,那么﹣16cm表示 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“同旁内角互补”的逆命题是_____________________,它是_____命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD 中,∠A∶∠B∶∠C∶∠D 的值可能是( )
A. 2∶5∶2∶5 B. 3∶4∶4∶5 C. 4∶4∶3∶2 D. 2∶3∶5∶6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,ABCD中,E、F分别是AD,BC的中点.求证:

(1)△AFB≌△CED;
(2)四边形AECF是平行四边形.
相关试题

