【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.

参考答案:
【答案】(1)证明见解析(2)3
【解析】试题分析:
(1)由AB=CD,BE=CF,可证Rt△BAE≌Rt△CDF,从而证得BE∥CF,即可得证;
(2)由题意可知∠2=30°,∠1=∠3=60°,在直角△ABE中求出AE,BE,在直角△BEC中求出BC的长,即可求出ED的长.
试题解析:
(1)证明:
∵四边形ABCD是矩形,∴∠A=∠CDF=∠ABC=90°,AB=DC,AD=BC,
在Rt△BAE和Rt△CDF中,
![]() ,
,
∴Rt△BAE≌Rt△CDF,∴∠1=∠F,∴BE∥CF,
又∵BE=CF,∴四边形EBCF是平行四边形.
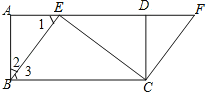
(2)解:∵Rt△BAE中,∠2=30°,AB=![]() ,
,
∴AE=ABtan∠2=1,![]() ,∠3=60°,
,∠3=60°,
在Rt△BEC中,![]() ,
,
∴AD=BC=4,
∴ED=AD﹣AE=4﹣1=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③
 (∠A+∠B)④
(∠A+∠B)④ (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两支清雪队同时开始清理某路段积雪,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的清雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨)与清雪时间x(时)之间的函数图象如图所示.
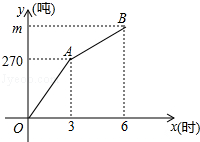
(1)乙队调离时,甲、乙两队已完成的清雪总量为吨;
(2)求此次任务的清雪总量m;
(3)求乙队调离后y与x之间的函数关系式. -
科目: 来源: 题型:
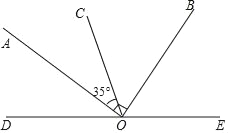
查看答案和解析>>【题目】如图,O,D,E三点在同一直线上,∠AOB=90°.
(1)图中∠AOD的补角是_____,∠AOC的余角是_____;
(2)如果OB平分∠COE,∠AOC=35°,请计算出∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON= ;∠CON= .
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=5°,求∠AOM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

相关试题

