【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB. 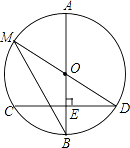
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
参考答案:
【答案】
(1)解:设⊙O的半径为x,则OE=x﹣8,
∵CD=24,由垂径定理得,DE=12,
在Rt△ODE中,OD2=DE2+OE2,
x2=(x﹣8)2+122,
解得:x=13
(2)解:∵OM=OB,
∴∠M=∠B,
∴∠DOE=2∠M,
又∠M=∠D,
∴∠D=30°,
在Rt△OED中,∵DE=12,∠D=30°,
∴OE=4 ![]()
【解析】(1)根据垂径定理求出DE的长,设出半径,根据勾股定理,列出方程求出半径;(2)根据OM=OB,证出∠M=∠B,根据∠M=∠D,求出∠D的度数,根据锐角三角函数求出OE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1,黏合部分的长度为4cm.若长为30cm,宽为10cm的长方形白纸条共有100张,则小明应分配到 张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
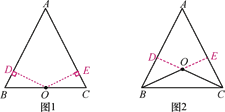
(1)如图1,若点O在BC上,求证:AB=AC.
(2)如图2,若点O在△ABC内部,求证:AB=AC.
(3)猜想,若点O在△ABC的外部,AB=AC成立吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A1、A2、A3、…、An(n为正整数)都在数轴上.点A2在点A1的左边,且A1A2=1;点A3在点A2的右边,且A2A3=2;点A4在点A3的左边,且A3A4=3;…,点A2018在点A2017的左边,且A2017A2018=2017,若点A2018所表示的数为2018,则点A1所表示的数为_____.
-
科目: 来源: 题型:
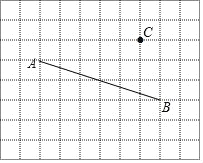
查看答案和解析>>【题目】利用网格画图:
(1)过点C画AB的平行线;
(2)过点C画AB的垂线,垂足为E;
(3)连接CA、CB,在线段CA、CB、CE中, 线段最短,理由: ;
(4)点C到直线AB的距离是线段的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量
单价(元/m3)
不超出80m3的部分
2.5
超出80m3不超出130m3的部分
a
超出130m3的部分
a+0.5
(1)若甲用户3月份用气125m3,缴费335元,求a的值;
(2)在(1)的条件下,若乙用户3月份缴费392元,则乙用户3月份的用气量是多少?
相关试题

