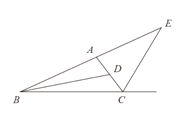
【题目】如图,△ABC中,BD为内角平分线,CE为外角平分线,若∠BDC=130°,∠E=50°,则∠BAC的度数为__________
参考答案:
【答案】120°.
【解析】
根据三角形的一个外角等于与它不相邻的两个内角的和以及CE是外角的平分线列式求出∠B的度数,再根据BD为内角平分线求出∠ABD的度数,然后利用三角形的外角性质即可求出∠BAC的度数.
根据三角形的外角性质,∠DBC+∠BDC=2(∠ABC+∠E),
∵BD为内角平分线,
∴∠DBC=∠ABD,
∴![]() ∠ABC+130°=2(∠ABC+50°),
∠ABC+130°=2(∠ABC+50°),
解得:∠ABC=20°,
∴∠ABD=![]() ×20°=10°,
×20°=10°,
在△ABD中,∠BDC=∠ABD+∠BAC,
即130°=10°+∠BAC,
解得∠BAC=120°.
故答案为:120°.
-
科目: 来源: 题型:
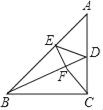
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线,E是AB上一点,且AE=AD,连接ED,作EF⊥BD于F,连接CF.则下面的结论:
①CD=CF;
②∠EDF=45°;
③∠BCF=45°;
④若CD=4,AD=5,则S△ADE=10.其中正确结论的个数是( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行了一次测试(满分50分,成绩均记为整数分),并按测试成绩m(单位:分)分成四类:A类(45<m≤50),B类(40<m≤45),C类(35<m≤40),D类(m≤35)绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
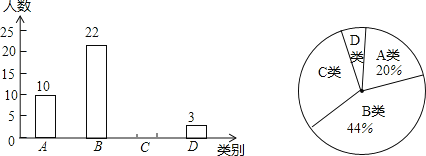
(1)求本次抽取的样本容量和扇形统计图中A类所对的圆心角的度数;
(2)若该校九年级男生有500名,D类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上
 两点对应的数分别为
两点对应的数分别为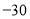 、16,点
、16,点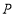 为数轴上一动点,点
为数轴上一动点,点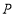 对应的数为
对应的数为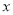 .
.(1)填空:若
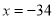 时,点
时,点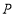 到点
到点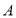 、点
、点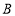 的距离之和为_____________.
的距离之和为_____________.(2)填空:若点
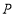 到点
到点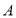 、点
、点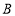 的距离相等,则
的距离相等,则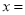 _______.
_______.(3)填空:若
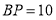 ,则
,则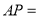 _______.
_______.(4)若动点
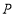 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点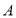 向点
向点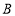 运动,动点
运动,动点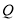 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点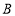 向点
向点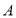 运动两动点同时运动且一动点到达终点时另一动点也停止运动,经过
运动两动点同时运动且一动点到达终点时另一动点也停止运动,经过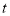 秒
秒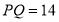 ,求
,求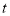 的值.
的值.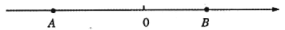
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠A=90°.
(1)请在图1中作出BC边上的中线(保留作图痕迹,不写作法);
(2)如图2,设BC边上的中线为AD,求证:BC=2AD.

-
科目: 来源: 题型:
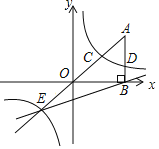
查看答案和解析>>【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB═
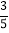 ,反比例函数y=
,反比例函数y=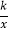 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为 .
.(1)求反比例函数的解析式;
(2)求直线EB的解析式;
(3)求S△OEB.
-
科目: 来源: 题型:
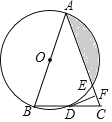
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
相关试题

