【题目】如图,数轴上![]() 两点对应的数分别为
两点对应的数分别为![]() 、16,点
、16,点![]() 为数轴上一动点,点
为数轴上一动点,点![]() 对应的数为
对应的数为![]() .
.
(1)填空:若![]() 时,点
时,点![]() 到点
到点![]() 、点
、点![]() 的距离之和为_____________.
的距离之和为_____________.
(2)填空:若点![]() 到点
到点![]() 、点
、点![]() 的距离相等,则
的距离相等,则![]() _______.
_______.
(3)填空:若![]() ,则
,则![]() _______.
_______.
(4)若动点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向点
向点![]() 运动,动点
运动,动点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 向点
向点![]() 运动两动点同时运动且一动点到达终点时另一动点也停止运动,经过
运动两动点同时运动且一动点到达终点时另一动点也停止运动,经过![]() 秒
秒![]() ,求
,求![]() 的值.
的值.
![]()
参考答案:
【答案】(1)54;(2)![]() ;(3)56或36;(4)
;(3)56或36;(4)![]() 的值为
的值为![]() 或12
或12
【解析】
(1)根据数轴上两点的距离公式即可求解;
(2)根据数轴上两点的中点公式即可求解;
(3)根据![]() 求出P点表示的数,故可得到AP的长;
求出P点表示的数,故可得到AP的长;
(4)根据P,Q的运动速度及![]() 分P,Q相遇前和相遇后分别列方程求解.
分P,Q相遇前和相遇后分别列方程求解.
(1) ![]() 时,点
时,点![]() 到点
到点![]() 、点
、点![]() 的距离之和为
的距离之和为![]() =54
=54
故答案为:54;
(2)若点![]() 到点
到点![]() 、点
、点![]() 的距离相等,则x=
的距离相等,则x=![]() =-7
=-7
故答案为:![]() ;
;
(3)∵![]()
∴P点表示的数为:6或26
则![]() 6-(-30)=36或26-(-30)=56
6-(-30)=36或26-(-30)=56
即AP=36或56
故答案为:56或36;
(4)解:∵![]()
当P,Q相遇前,得![]()
解得![]()
当P,Q相遇后,得![]() 时
时
解得![]()
![]() 的值为
的值为![]() 或12.
或12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在城市已基本普及,为满足消费者需求,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、标价如下表:
进价(元/只)
标价(元/只)
甲型
25
40
乙型
45
60
(1)如何进货才能保证进货款恰好为46000元?
(2)由于恰逢五一,商场决定搞促销活动,乙型节能灯打八五折,请你运用所学的知识预算一下甲型节能灯要打几折才能使这批灯售完后获得9200元的利润(不考虑其它因素)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线,E是AB上一点,且AE=AD,连接ED,作EF⊥BD于F,连接CF.则下面的结论:
①CD=CF;
②∠EDF=45°;
③∠BCF=45°;
④若CD=4,AD=5,则S△ADE=10.其中正确结论的个数是( )
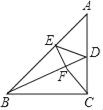
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行了一次测试(满分50分,成绩均记为整数分),并按测试成绩m(单位:分)分成四类:A类(45<m≤50),B类(40<m≤45),C类(35<m≤40),D类(m≤35)绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
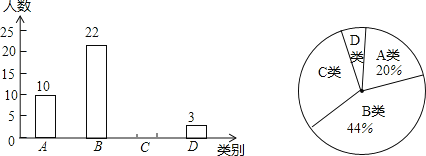
(1)求本次抽取的样本容量和扇形统计图中A类所对的圆心角的度数;
(2)若该校九年级男生有500名,D类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BD为内角平分线,CE为外角平分线,若∠BDC=130°,∠E=50°,则∠BAC的度数为__________
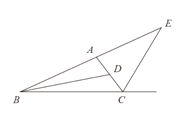
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠A=90°.
(1)请在图1中作出BC边上的中线(保留作图痕迹,不写作法);
(2)如图2,设BC边上的中线为AD,求证:BC=2AD.

-
科目: 来源: 题型:
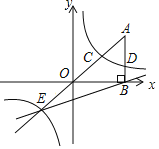
查看答案和解析>>【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB═
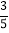 ,反比例函数y=
,反比例函数y=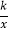 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为 .
.(1)求反比例函数的解析式;
(2)求直线EB的解析式;
(3)求S△OEB.
相关试题

