【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A,B,C三点; 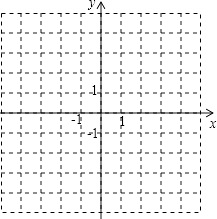
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.
参考答案:
【答案】
(1)解:如图所示:

(2)解:由图形可得:AB=2,AB边上的高=|﹣1|+|4|=5,
∴△ABC的面积= ![]() AB×5=5
AB×5=5
(3)解:∵A(0,4),B(2,4),C(3,﹣1),△A1B1C1与△ABC关于x轴对称,
∴A1(0,﹣4)、B1(2,﹣4)、C1.(3,1)
【解析】(1)根据三点的坐标,在直角坐标系中分别标出位置即可.(2)以AB为底,则点C到AB得距离即是底边AB的高,结合坐标系可得出高为点C的纵坐标的绝对值加上点B的纵坐标的绝对值,从而根据三角形的面积公式计算即可.(3)关于x轴对称的点的坐标,横坐标不变,纵坐标互为相反数,从而可得出A1、B1、C1的坐标.
【考点精析】关于本题考查的作轴对称图形,需要了解画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m2﹣2m﹣1=0,则2m2﹣4m+3= .
-
科目: 来源: 题型:
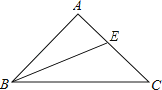
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,BE平分∠ABC交AC于E,若∠A=90°,那么BC、BA、AE三者之间有何关系?并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品的商标如图所示,O是线段AC,DB的交点,且AC=BD,AB=DC,小华认为图中的两个三角形全等,他的思考过程是:
∵AC=DB,∠AOB=∠DOC,AB=AC,
∴△ABO≌△DCO
你认为小华的思考过程对吗?如果正确,指出他用的是判别三角形全等的哪个条件;如果不正确,写出你的思考过程.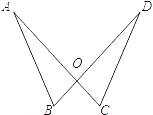
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
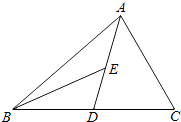
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜用普查的是 ( )
A. 某品牌灯泡的使用寿命 B. 了解公民保护环境的意识
C. 长江中现有鱼的种类 D. 审核书稿中的错别字
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x2+4x+n-3=0有两个不相等的实数根,则n的取值范围是_________.
相关试题

