【题目】已知A、B在数轴上对应的数分别用a、b表示,且(b+10)2+|a﹣20|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离.
(2)当P点满足PB=2PA时,求P点对应的数.
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,依此类推,…点P能够移到与A、B重合的位置吗?若能,请探索第几次移动时重合;若不能,请说明理由.
参考答案:
【答案】(1)AB=30;(2)P点对应的数为10或50;(3)第20次P与A重合;点P与点B不重合,理由见解析.
【解析】试题分析:(1)先根据非负数的性质求出a,b的值,在数轴上表示出A、B的位置,根据数轴上两点间的距离公式,求出A、B之间的距离即可;
(2)设P点对应的数为x,当P点满足PB=2PA时,分三种情况讨论,根据PB=2PA求出x的值即可;
(3)根据第一次点P表示﹣1,第二次点P表示2,点P表示的数依次为﹣3,4,﹣5,6…,找出规律即可得出结论.
试题解析:(1)∵(b+10)2+|a﹣20|=0,
∴b+10=0,a﹣20=0,
∴b=﹣10,a=20.
A、B的位置如图所示:
![]()
∴AB=|﹣10﹣20|=30;
(2)设P点对应的数为x,当P点满足PB=2PA时,分三种情况讨论:
①若点P在点B的左侧,则PB<PA,与PB=2PA不符,舍去;
②若点P在AB之间,则x﹣(﹣10)=2(20﹣x),
解得x=10;
③若点P在点A的右侧,则x﹣(﹣10)=2(x﹣20),
解得x=50,
综上所述,P点对应的数为10或50;
(3)由题可得,第一次点P表示﹣1,第二次点P表示2,点P表示的数依次为﹣3,4,﹣5,6…,
∴第n次为(﹣1)nn,
∵点A表示20,点B表示﹣10,
∴当n=20时,(﹣1)nn=20;
当n=10时,(﹣1)nn=10≠﹣10,
∴第20次P与A重合;点P与点B不重合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种药品原价为49元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A.49(1﹣x)2=49﹣25
B.49(1﹣2x)=25
C.49(1﹣x)2=25
D.49(1﹣x2)=25 -
科目: 来源: 题型:
查看答案和解析>>【题目】小刚位于A点,在学校正北方向5 km处,记作+5;小敏位于B点,在学校正南方向3 km处,记作-3.小刚和小敏沿AB所在直线同时行进2 km,他俩相距________km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边△ABC内接于⊙O,AD为O的直径交线段BC于点M,DE∥BC,交AB的延长线于点E.
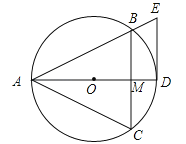
(1)求证:DE是⊙O的切线;
(2)若等边△ABC的边长为6,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
问题:如图所示,在正方形ABCD和BEFG中,点A,B,E在同一直线上,P是线段DF中点,连接PG,PC.
探究:当PG与PC的夹角为90°时,平行四边形BEFG是正方形.
小聪同学的思路是:首先可以证明四边形BEFG是矩形,然后延长GP交DC于点H,构造全等三角形,经过推理可以探索出问题答案.
请你参考小聪同学的思路,探究并解决这个问题.
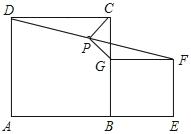
(1)求证:四边形BEFG是矩形;
(2)求证:PG与PC的夹角为90°时,四边形BEFG是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市参加中考的25000名学生的身高情况,抽查了其中1200名学生的身高进行统计分析.下面叙述正确的是( )
A.25000名学生是总体 B.1200名学生的身高是总体的一个样本
C.每名学生是总体的一个个体 D.以上调查是全面调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3x4﹣x2=3x2
B.(﹣2ab3)2a=4a3b6
C.8a6÷2a3=4a2
D.(a﹣2)2=a2﹣4
相关试题

