【题目】已知等边△ABC内接于⊙O,AD为O的直径交线段BC于点M,DE∥BC,交AB的延长线于点E.
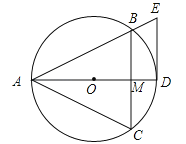
(1)求证:DE是⊙O的切线;
(2)若等边△ABC的边长为6,求BE的长.
参考答案:
【答案】(1)证明见解析(2)2
【解析】
试题分析:(1)由等边三角形的性质得出O即是△ABC的外心,又是△ABC的内心,得出∠BAM=∠CAM=30°,因此∠AMB=90°,由平行线的性质得出∠EDA=90°,即可得出结论;
(2)由等边三角形的性质得出BM=![]() AB=3,连接OB,则∠OBM=30°,得出OM=
AB=3,连接OB,则∠OBM=30°,得出OM=![]() OB,由勾股定理求出OB,由平行线的性质得出
OB,由勾股定理求出OB,由平行线的性质得出![]() =
=![]() ,求出AE,即可得出BE的长.
,求出AE,即可得出BE的长.
(1)证明:∵等边△ABC内接于⊙O,
∴∠ABC=60°,O即是△ABC的外心,又是△ABC的内心,
∴∠BAM=∠CAM=30°,
∴∠AMB=90°,
∵DE∥BC,
∴∠EDA=∠AMB=90°,
∵AD为⊙O的直径,
∴DE是⊙O的切线;
(2)解:∵△ABC是等边三角形,
∴BM=![]() AB=3,
AB=3,
连接OB,如图所示:
则∠OBM=30°,
∴OM=![]() OB,
OB,
由勾股定理得:OB2﹣OM2=BM2,
即OB2﹣(![]() OB)2=32,
OB)2=32,
解得:OB=2![]() ,
,
∴OM=![]() ,AM=3
,AM=3![]() ,AD=4
,AD=4![]() ,
,
∵DE∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:AE=8,
∴BE=AE﹣AB=8﹣6=2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“x的2倍的相反数”用代数式表示为 _________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种药品原价为49元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A.49(1﹣x)2=49﹣25
B.49(1﹣2x)=25
C.49(1﹣x)2=25
D.49(1﹣x2)=25 -
科目: 来源: 题型:
查看答案和解析>>【题目】小刚位于A点,在学校正北方向5 km处,记作+5;小敏位于B点,在学校正南方向3 km处,记作-3.小刚和小敏沿AB所在直线同时行进2 km,他俩相距________km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B在数轴上对应的数分别用a、b表示,且(b+10)2+|a﹣20|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离.
(2)当P点满足PB=2PA时,求P点对应的数.
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,依此类推,…点P能够移到与A、B重合的位置吗?若能,请探索第几次移动时重合;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
问题:如图所示,在正方形ABCD和BEFG中,点A,B,E在同一直线上,P是线段DF中点,连接PG,PC.
探究:当PG与PC的夹角为90°时,平行四边形BEFG是正方形.
小聪同学的思路是:首先可以证明四边形BEFG是矩形,然后延长GP交DC于点H,构造全等三角形,经过推理可以探索出问题答案.
请你参考小聪同学的思路,探究并解决这个问题.
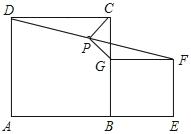
(1)求证:四边形BEFG是矩形;
(2)求证:PG与PC的夹角为90°时,四边形BEFG是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市参加中考的25000名学生的身高情况,抽查了其中1200名学生的身高进行统计分析.下面叙述正确的是( )
A.25000名学生是总体 B.1200名学生的身高是总体的一个样本
C.每名学生是总体的一个个体 D.以上调查是全面调查
相关试题

