【题目】某市射击队甲、乙两名优秀队员在相同的条件下各射耙![]() 次,每次射耙的成绩情况如图所示:
次,每次射耙的成绩情况如图所示:

![]() 请将表格补充完整:
请将表格补充完整:
平均数 | 方差 | 中位数 | 命中 | |
甲 |
|
|
| |
乙 |
|
![]() 请从下列四个不同的角度对这次测试结果进行
请从下列四个不同的角度对这次测试结果进行
①从平均数和方差向结合看,________的成绩好些;
②从平均数和中位数相结合看,________的成绩好些;
③从平均数和折线统计图走势相结合看,________的成绩好些;
④若其他队选手最好成绩在![]() 环左右,现要选一人参赛,你认为选谁参加,并说明理由.
环左右,现要选一人参赛,你认为选谁参加,并说明理由.
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ,(2)①甲,②乙,③乙;④乙.
,(2)①甲,②乙,③乙;④乙.
【解析】
(1)分别根据方差公式、中位数的定义以及算术平均数的计算方法进行计算即可得.(2)分别根据平均数、方差、中位数的意义解答即可.
解;(1)甲:方差=![]() [(9-7)2+(5-7)2+(7-7)2+(8-7)2+(7-7)2+(6-7)2+(8-7)2+(6-7)2+(7-7)2+(7-7)2],
[(9-7)2+(5-7)2+(7-7)2+(8-7)2+(7-7)2+(6-7)2+(8-7)2+(6-7)2+(7-7)2+(7-7)2],
=1.2;
成绩按照从小到大的顺序排列如下:5、6、6、7、7、7、7、7、8、8、9,
第5、6两个数都是7,
所以,中位数是7;
命中9环以上的有1环;
乙:平均数=![]() (2+4+6+8+7+7+8+9+9+10)=
(2+4+6+8+7+7+8+9+9+10)=![]() ×70=7,
×70=7,
成绩按照从小到大的顺序排列如下:2、4、6、7、7、8、8、9、9、10,
第5个数是7,第6个数是8,
所以,中位数是![]() (7+8)=7.5;
(7+8)=7.5;
命中9环以上的有3次;
填表如下:
平均数 | 方差 | 中位数 | 命中9环以上的环数 | |
甲 | 7 | 1.2 | 7 | 1 |
乙 | 7 | 5.4 | 7.5 | 3 |
(2)①从平均数和方差结合看:甲的成绩好些;
因为,甲、乙的平均数一样,而甲的方差小,成绩比乙更稳定;
②从平均数和中位数相结合看:乙的成绩稍微好.
因为,两人的平均数相同,乙的中位数稍微高;
③从平均数和命中9环以上的次数结合看:乙的成绩好些.
因为,甲、乙的平均数一样,而乙的方命中9环以上的次数有3次,而甲只有1次;
④综合看,甲发挥更稳定,但射击精准度差;乙发挥虽不稳定,但击中高靶环次数更多,成绩提高潜力大,更具有培养价值.应选乙.
-
科目: 来源: 题型:
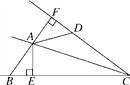
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A. ①②④ B. ②③④
C. ①②③ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店一周内甲、乙两种计算器每天的销售量如下(单位:个):
类别/星期
一
二
三
四
五
六
七
平均数
甲
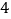
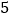
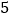
乙
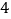
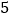
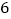
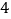
(1)将表格填写完整.
(2)求甲种计算器本周销售量的方差.
(3)已知乙种计算器本周销售量的方差为
 ,本周哪种计算器的销售量比较稳定?说明理由.
,本周哪种计算器的销售量比较稳定?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某生产小组有
 名工人,调查每个工人的日均零件生产能力,获得如表数据:
名工人,调查每个工人的日均零件生产能力,获得如表数据:日均生产零件的个数(个)






工人人数(人)






 求这
求这 名工人日均生产零件的众数、中位数、平均数.
名工人日均生产零件的众数、中位数、平均数. 为提高工作效率和工人的工作积极性,生产管理者准备实行“每天定额生产,超产有奖”的措施,如果你是管理者,你将如何确定这个定额?请说明理由.
为提高工作效率和工人的工作积极性,生产管理者准备实行“每天定额生产,超产有奖”的措施,如果你是管理者,你将如何确定这个定额?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】将数轴按如图所示从点A开始折出一等边△ABC,设A表示的数为x-3, B表示的数为2x-5,C表示的数为5-x,则x=_______.将△ABC向右滚动,则点2016与点_____重合.(填A.B.C)

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:在数学课上,老师提出如下问题:
尺规作图,过圆外一点作圆的切线.
已知:⊙O和点P
求过点P的⊙O的切线小涵的主要作法如下:
如图,(1)连结OP,作线段OP的中点A;
(2)以A为圆心,OA长为半径作圆,交⊙O于点B,C;
(3)作直线PB和PC.
所以PB和PC就是所求的切线.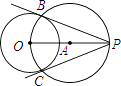
老师说:“小涵的做法是正确的.”
请回答:小涵的作图依据是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.
(1)若∠ABE=60°,求∠CDA的度数;
(2)若AE=2,BE=1,CD=4.求四边形AECD的面积.
相关试题

