【题目】如图, ![]() 的图像交x轴于O点和A点,将此抛物线绕原点旋转180°得图像y2 , y2与x轴交于O点和B点.
的图像交x轴于O点和A点,将此抛物线绕原点旋转180°得图像y2 , y2与x轴交于O点和B点.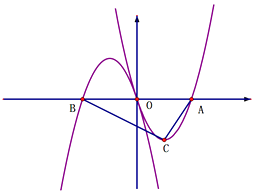
(1)若y1=2x2-3x,则y2= .
(2)设 y 1 的顶点为C,则当△ABC为直角三角形时,请你任写一个符合此条件的 y 1 的表达式 .
参考答案:
【答案】
(1)y1=-2x2-3x
(2)y1=![]() (x-1)2-
(x-1)2-![]()
【解析】(1)解:y1=2x2-3x的图像交x轴于O点和A点,![]()
∴O(0,0),A(![]() ,0),
,0),
又∵将y1绕原点旋转180°得图像y2,
∴B(-![]() ,0),
,0),
∴y2解析式为:y1=-2x2-3x.
(2)依据题意得:y1=![]() (x-1)2-
(x-1)2-![]()
【考点精析】掌握勾股定理的概念是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个小组同时从山脚开始攀登一座600m高的山,第一小组的攀登速度(即攀登高度与攀登时间之比)是第二小组的1.2倍,并比第二小组早20min到达山顶.
(1)第二小组的攀登速度是多少?
(2)如果山高为hm,第一小组的攀登速度是第二小组的k(k>1)倍,并比第二小组早tmin到达山顶,则第一小组的攀登速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】宜宾某商店决定购进A.B两种纪念品.购进A种纪念品7件,B种纪念品2件和购进A种纪念品5件,B种纪念品6件均需80元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于750元,但不超过764元,那么该商店共有几种进货方案?
(3)已知商家出售一件A种纪念品可获利a元,出售一件B种纪念品可获利(5﹣a)元,试问在(2)的条件下,商家采用哪种方案可获利最多?(商家出售的纪念品均不低于成本价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据表中的信息判断,下列语句中正确的是( )
x
15
15.1
15.2
15.3
15.4
15.5
15.6
15.7
15.8
15.9
16
x2
225
228.01
231.04
234.09
237.16
240.25
243.36
246.49
249.64
252.81
256
A.

B.235的算术平方根比15.3小
C.只有3个正整数n满足15.5
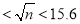
D.根据表中数据的变化趋势,可以推断出16.12将比256增大3.19
-
科目: 来源: 题型:
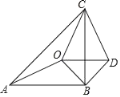
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,AB=BC,O是△ABC内部的一个动点,△OBD是等腰直角三角形,OB=BD.
(1)求证:∠AOB=∠CDB;
(2)若△COD是等腰三角形,∠AOC=140°,求∠AOB的度数.
-
科目: 来源: 题型:
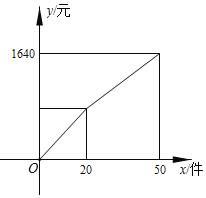
查看答案和解析>>【题目】某商店有一款畅销服装原价为40元,该商店规定:若顾客购买服装数量在20件以内,则按原价进行销售:若顾客购买服装数量超过20件,超过的部分每件可以享受指定的折扣,现八
 班同学为参加学校秋季运动会,准备统一向该商店购买该款服装,所需费用
班同学为参加学校秋季运动会,准备统一向该商店购买该款服装,所需费用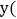 元
元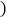 与购买数量
与购买数量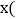 件
件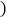 之间的函数关系如图所示,那么购买数量超过20件的部分每件享受到的折扣是
之间的函数关系如图所示,那么购买数量超过20件的部分每件享受到的折扣是
A. 9折B. 8折C.
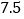 折D. 7折
折D. 7折 -
科目: 来源: 题型:
查看答案和解析>>【题目】一袋子中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋子中任取一个小球,对应的数字作为一个两位数的十位数;然后将小球放回袋子中并搅拌均匀,再任取一个小球,对应数字作为这个两位数的的个位数.
(1)用树状图或列表的方法,写出按照上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
相关试题

