【题目】一袋子中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋子中任取一个小球,对应的数字作为一个两位数的十位数;然后将小球放回袋子中并搅拌均匀,再任取一个小球,对应数字作为这个两位数的的个位数.
(1)用树状图或列表的方法,写出按照上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
参考答案:
【答案】
(1)解:列表得:
1 | 4 | 7 | 8 | |
1 | 11 | 41 | 71 | 81 |
4 | 14 | 44 | 74 | 84 |
7 | 17 | 47 | 77 | 87 |
8 | 18 | 48 | 78 | 88 |
由表可知得到所有可能的两位数共16个.
(2)解:∵ 4<![]() <7 ,
<7 ,
∴ 16<a<49 .
∴可以选择的数为6个.
∴ 算术平方根大于4且小于7的概率为:![]() =
=![]() .
.
【解析】(1)根据题意列出所有可能得到的两位数.
(2)算术平方根大于4且小于7的数有6个,从而求出满足条件额概率.
【考点精析】解答此题的关键在于理解列表法与树状图法的相关知识,掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率,以及对概率公式的理解,了解一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
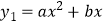 的图像交x轴于O点和A点,将此抛物线绕原点旋转180°得图像y2 , y2与x轴交于O点和B点.
的图像交x轴于O点和A点,将此抛物线绕原点旋转180°得图像y2 , y2与x轴交于O点和B点.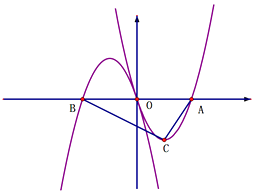
(1)若y1=2x2-3x,则y2= .
(2)设 y 1 的顶点为C,则当△ABC为直角三角形时,请你任写一个符合此条件的 y 1 的表达式 . -
科目: 来源: 题型:
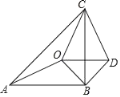
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,AB=BC,O是△ABC内部的一个动点,△OBD是等腰直角三角形,OB=BD.
(1)求证:∠AOB=∠CDB;
(2)若△COD是等腰三角形,∠AOC=140°,求∠AOB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店有一款畅销服装原价为40元,该商店规定:若顾客购买服装数量在20件以内,则按原价进行销售:若顾客购买服装数量超过20件,超过的部分每件可以享受指定的折扣,现八
 班同学为参加学校秋季运动会,准备统一向该商店购买该款服装,所需费用
班同学为参加学校秋季运动会,准备统一向该商店购买该款服装,所需费用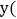 元
元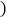 与购买数量
与购买数量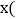 件
件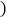 之间的函数关系如图所示,那么购买数量超过20件的部分每件享受到的折扣是
之间的函数关系如图所示,那么购买数量超过20件的部分每件享受到的折扣是
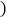
A. 9折B. 8折C.
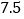 折D. 7折
折D. 7折 -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机店今年1-4月的手机销售总额如图1,其中一款音乐手机的销售额占当月手机销售总额的百分比如图2.有以下四个结论:
①从1月到4月,手机销售总额连续下降
②从1月到4月,音乐手机销售额在当月手机销售总额中的占比连续下降
③音乐手机4月份的销售额比3月份有所下降
④今年1-4月中,音乐手机销售额最低的是3月
其中正确的结论是________(填写序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】小华和小峰是两名自行车爱好者,小华的骑行速度比小峰快
 两人准备在周长为250米的赛道上进行一场比赛
两人准备在周长为250米的赛道上进行一场比赛 若小华在小峰出发15秒之后再出发,图中
若小华在小峰出发15秒之后再出发,图中 、
、 分别表示两人骑行路程与时间的关系.
分别表示两人骑行路程与时间的关系. 小峰的速度为______米
小峰的速度为______米 秒,他出发______米后,小华才出发;
秒,他出发______米后,小华才出发; 小华为了能和小峰同时到达终点,设计了两个方案,方案一:加快骑行速度;方案二:比预定时间提前出发.
小华为了能和小峰同时到达终点,设计了两个方案,方案一:加快骑行速度;方案二:比预定时间提前出发. 图______
图______ 填“A“”或“B“
填“A“”或“B“ 代表方案一;
代表方案一; 若采用方案二,小华必须在小峰出发多久后开始骑行?求出此时小华骑行的路程与时间的函数关系式.
若采用方案二,小华必须在小峰出发多久后开始骑行?求出此时小华骑行的路程与时间的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
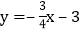 交x轴于点A,交y轴于点B,交直线
交x轴于点A,交y轴于点B,交直线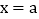 于点C,点D与点B关于x轴对称,连接AD交直线
于点C,点D与点B关于x轴对称,连接AD交直线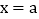 于点E.
于点E. 填空:
填空: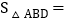 ______.
______. 求直线AD的解析式;
求直线AD的解析式; 在x轴上存在一点P,则
在x轴上存在一点P,则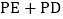 的和最小为______;
的和最小为______; 直接填空即可
直接填空即可
 当
当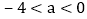 时,点Q为y轴上的一个动点,使得
时,点Q为y轴上的一个动点,使得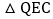 为等腰直角三角形,求点Q的坐标.
为等腰直角三角形,求点Q的坐标.
相关试题

