【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。则图中阴影部分的面积是( )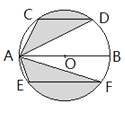
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:作GH⊥AB,交CD于G,交EF于H,连接OC、OD、OE、OF.
∵⊙O的直径AB=10,CD=6,EF=8,且AB‖CD‖EF,
∴OG⊥CD,OH⊥EF,
∴∠COG=∠DOG,∠EOH=∠FOH,
∴OE=OF=OC=OD=5,CG=3,EH=4,
∴OG=4,OH=3,
∵AB‖CD‖EF,
∴S△OCD=S△BCD , S△OEF=S△BEF ,
∴S阴影=S扇形ODC+S扇形OEF=S半圆=![]() π×52=
π×52=![]() π.
π.
故答案是:![]() π.
π.
【考点精析】解答此题的关键在于理解垂径定理的推论的相关知识,掌握推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A在函数
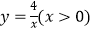 的图象上,AB⊥
的图象上,AB⊥ 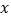 轴于点B,AB的垂直平分线与
轴于点B,AB的垂直平分线与 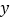 轴交于点C,与函数
轴交于点C,与函数 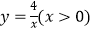 的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )
的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )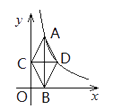
A. 2
B.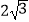
C.4
D.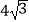
-
科目: 来源: 题型:
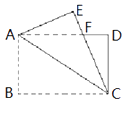
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
A.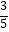
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )

A. 点A B. 点B
C. A,B之间 D. B,C之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM,ON分别是∠AOC,∠BOD的平分线,∠MON等于________.

-
科目: 来源: 题型:
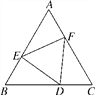
查看答案和解析>>【题目】如图,在△ABC中,∠B=∠C,点D为BC边上(B,C点除外)的动点,∠EDF的两边与AB,AC分别交于点E,F,且BD=CF,BE=CD.
(1)求证:DE=DF;
(2)若∠EDF=m,用含m的代数式表示∠A的度数;
(3)连接EF,求当△DEF为等边三角形时∠A的度数.
相关试题

