【题目】综合题
(1)如图,已知△ABC中,AD⊥BC于D, AE为∠BAC的平分线,∠B=50°,∠C=70°,求∠DAE的度数.
(2)已知在△ABC中,AD⊥BC于点D,AE平分∠BAC(∠C>∠B).求证:∠DAE= ![]() (∠C-∠B).
(∠C-∠B).
参考答案:
【答案】
(1)解:∵∠B=50°,∠C=70°,
∴∠BAC=60°
∵AE平分∠BAC
∴∠EAC=60°÷2=30°
∵AD⊥BC
∴∠ADC=90°
∴∠DAC=180°-90°-70°=20°
∴∠DAE=∠EAC-∠DAC=30°-20°=10°
(2)解:∵AE平分∠BAC(已知),
∴∠EAC= ![]() ∠BAC
∠BAC
∵∠BAC+∠B+∠C=180°
∴∠BAC=180°-∠B-∠C
∴∠EAC= ![]() (180°-∠B-∠C).
(180°-∠B-∠C).
∵AD⊥BC(已知),
∴∠ADC=90° 在△ADC中,∠ADC+∠C+∠DAC=180°
∴∠DAC=180°-∠ADC-∠C(等式性质)=90°-∠C.
∴∠EAD=∠EAC-∠DAC= ![]() (180°-∠B-∠C)-(90°-∠C)
(180°-∠B-∠C)-(90°-∠C)
= ![]() (180°-∠B-∠C)-
(180°-∠B-∠C)- ![]() (180°-2∠C)=
(180°-2∠C)= ![]() (180°-∠B-∠C-180°+2∠C)=
(180°-∠B-∠C-180°+2∠C)= ![]() (∠C-∠B)
(∠C-∠B)
【解析】(1)根据三角形的内角和定理,求出∠BAC的度数,根据角平分线的定义和角的和差,求出∠DAE的度数;(2)根据角平分线定义和三角形内角和定理以及角的和差,得到结论.
【考点精析】掌握三角形的“三线”和三角形的内角和外角是解答本题的根本,需要知道1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A=10a2+3b2﹣5a+5,B=a2+3b2﹣8a+5,则A﹣B的值与﹣9a3b2的公因式为( )
A.a
B.﹣3
C.9a3b2
D.3a -
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程
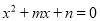 有两个不相等实数根的概率.
有两个不相等实数根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个)
…
160
200
240
300
…
每个玩具的固定成本Q(元)
…
60
48
40
32
…
(1)写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式b2(x﹣3)+b(x﹣3)的正确结果是( )
A.(x﹣3)(b2+b)
B.b(x﹣3)(b+1)
C.(x﹣3)(b2﹣b)
D.b(x﹣3)(b﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学进入初三后,某科6次考试成绩如图:
(1)请根据下图填写如表:平均数
方差
中位数
众数
极差
甲
75
75
乙
33.3
15
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析:
①从平均数和方差相结合看;
②从折线图上两名同学分数的走势上看,你认为反映出什么问题?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

相关试题

