搜索
【题目】如图，在四边形ABCD中，AD∥BC, AB=AC，BE=CE=AD.
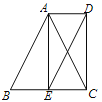
（1）求证：四边形ECDA是矩形；
（2）当△ABC是什么类型的三角形时，四边形ECDA是正方形？请说明理由.
参考答案：
【答案】(1)、证明过程见解析；(2)、当△ABC是等腰直角三角形时；证明过程见解析.
【解析】
试题分析：(1)、根据AD//EC且AD=EC得到平行四边形，然后根据AB=AC，BE=CE得出∠AEC=90°，则得到矩形；(2)、根据等腰直角三角形的性质得出AE=EC，从而得到正方形.
试题解析：(1)、在四边形AECD中,AD//EC且AD=EC. ∴ 四边形AECD是平行四边形
∵AB=AC，BE=CE ∴AE⊥BC ,∠AEC=90° ∴四边形AECD是矩形
、当△ABC是等腰直角三角形时，四边形ECDA是正方形
∵△ABC等腰直角三角形时，∠AEC=Rt∠,又因BE=CE ∴AE =
=CE
又∵四边形AECD是矩形 ∴四边形ECDA是正方形
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种细胞的直径是0.000067厘米，将0.000067用科学记数法表示为（ ）
A. 0.67×10-5 B. 67×10-6 C. 6.7×10-6 D. 6.7×10-5
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种商品每件的标价是330元，按标价的八折销售时，仍可获利10%，则这种商品每件的进价为（ ）
A. 200元 B. 240元 C. 250元 D. 300元
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1)如图1，等腰Rt△ABO放在平面直角坐标系中， 点A，B 的坐标分别是A(0，1)，B(1，0).在x轴正半轴上取D（m，0），在AD右上方作等腰Rt△ADE，∠ADE=
.
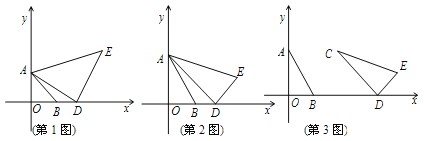
①求出E点的坐标(可用含m的代数式表示)；
②证明对于任意正数m，点E都在直线
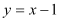上；(2)将(1)中的两个等腰直角三角形都改为有一个角为
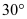的直角三角形,如图22-2，A(0,
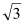)，B(1，0). Rt△ADE中, ∠ADE=,∠AED=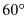
. D（m,0）是x轴正半轴上任意一点,则不论m取何正数，点E都在某一条直线上，请求出这条直线的函数关系式；(3)将(2)中Rt△AOB保持不动,取点C(2,
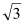),在x轴正半轴上取D（m,0）(m>2), 然后在AD右上方作Rt△CDE, ∠CDE=，∠CED=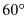.当m取不同值时，点E是否还是总在一条直线上? 若是，请求出直线对应的函数关系式，若不是，请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】数轴上两点A、B分别表示数－2和3，则A、B两点间的距离是 .
-
科目： 来源： 题型：
查看答案和解析>>【题目】过某个多边形一个顶点的所有对角线，将这个多边形分成7个三角形，这个多边形是 边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y＝-2x2-8x-6，当____时，y随x的增大而增大；当x＝____时，y有最____值是____.
相关试题
