【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,
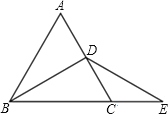
(1)求证:DB=DE.
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
参考答案:
【答案】(1)证明见解析(2)48
【解析】试题分析:(1)根据等边三角形的性质得到∠ABC=∠ACB=60°,∠DBC=30°,再根据角之间的关系求得∠DBC=∠CED,根据等角对等边即可得到DB=DE;(2)根据直角三角形中,30°的锐角所对的直角边等于斜边的一半DC=8,AC=16,即可求得△ABC的周长.
试题解析:
(1)证明:∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=![]() ∠BCD=30°.
∠BCD=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边);
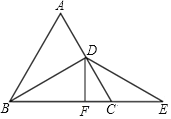
(2)解: ∵∠CDE=∠CED=![]() ∠BCD=30°,
∠BCD=30°,
∴∠CDF=30°,
∵CF=4,
∴DC=8,
∵AD=CD,
∴AC=16,
∴△ABC的周长=3AC=48.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论不正确的是( )
A. 有理数包括正数和负数 B. 无限不循环小数叫做无理数
C. 0是自然数 D. 互为相反数通常是原点两侧的数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ,CP,若AQ⊥CP,求t的值;
(3)试证明:PQ的中点在△ABC的一条中位线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E. F.

(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个n边形变成(n+2)边形,内角和将( )
A. 减少180B. 增加180°C. 减少360°D. 增加360°
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2–3x–a=0有一个实数根为–1,则a的值为( )
A. 2 B. –2 C. 4 D. –4
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三位选手各10次射击成绩的平均数和方差统计如表:
选手
甲
乙
丙
平均数
9.3
9.3
9.3
方差
0.026
a
0.032
已知乙是成绩最稳定的选手,且乙的10次射击成绩不都一样,则a的值可能是( )
A. 0B. 0.020C. 0.030D. 0.035
相关试题

