【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ,CP,若AQ⊥CP,求t的值;
(3)试证明:PQ的中点在△ABC的一条中位线上.
参考答案:
【答案】(1)t=1或![]() 时,△BPQ与△ABC相似;(2)t=
时,△BPQ与△ABC相似;(2)t=![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)分两种情况讨论:①当△BPQ∽△BAC时, ![]() ,当△BPQ∽△BCA时,
,当△BPQ∽△BCA时, ![]() ,再根据BP=5t,QC=4t,AB=10cm,BC=8cm,代入计算即可;
,再根据BP=5t,QC=4t,AB=10cm,BC=8cm,代入计算即可;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,MC=8-4t,根据△ACQ∽△CMP,得出![]() ,代入计算即可;
,代入计算即可;
(3)作PE⊥AC于点E,DF⊥AC于点F,先得出DF=![]() ,再把QC=4t,PE=8-CM=8-4t代入求出DF,过BC的中点R作直线平行于AC,得出RC=DF,D在过R的中位线上,从而证出PQ的中点在△ABC的一条中位线上.
,再把QC=4t,PE=8-CM=8-4t代入求出DF,过BC的中点R作直线平行于AC,得出RC=DF,D在过R的中位线上,从而证出PQ的中点在△ABC的一条中位线上.
试题解析:(1)∵AC=6cm,BC=8cm,
∴AB=![]() =10cm,
=10cm,
①当△BPQ∽△BAC时,
∵![]() ,BP=5t,QC=4t,AB=10cm,BC=8cm,
,BP=5t,QC=4t,AB=10cm,BC=8cm,
∴![]() ,
,
∴t=1;
②当△BPQ∽△BCA时,
∵![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
∴t=1或![]() 时,△BPQ与△ABC相似;
时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=PBsinB=3t,BM=4t,MC=8-4t,
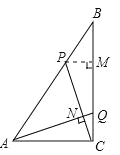
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴![]() ,
,
∴![]() ,
,
解得:t=![]() ;
;
(3)如图,作PM⊥BC于点M,PQ的中点设为D点,再作PE⊥AC于点E,DF⊥AC于点F,
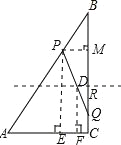
∵∠ACB=90°,
∴DF为梯形PECQ的中位线,
∴DF=![]() ,
,
∵QC=4t,PE=8-BM=8-4t,
∴DF=![]() =4,
=4,
∵BC=8,过BC的中点R作直线平行于AC,
∴RC=DF=4成立,
∴D在过R的中位线上,
∴PQ的中点在△ABC的一条中位线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A(a,3),B(1,b)关于x轴对称,则a+b=( )
A. 2B. -2C. 4D. -4
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一假期,黄石市退出了东方山休闲娱乐、传统文化展演、游园赏景赏花、佛教文化体验等精品文化活动,共接待旅游总人数9 608 00人次,将9 608 00用科学记数法表示为( )
A. 9608×102 B. 960.8×103 C. 96.08×104 D. 9.608×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论不正确的是( )
A. 有理数包括正数和负数 B. 无限不循环小数叫做无理数
C. 0是自然数 D. 互为相反数通常是原点两侧的数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E. F.

(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,
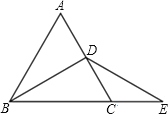
(1)求证:DB=DE.
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个n边形变成(n+2)边形,内角和将( )
A. 减少180B. 增加180°C. 减少360°D. 增加360°
相关试题

