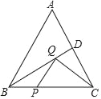
【题目】如图,等边△ABC的周长为18cm,BD为AC边上的中线,动点P,Q分别在线段BC,BD上运动,连接CQ,PQ,当BP长为_____cm时,线段CQ+PQ的和为最小.
参考答案:
【答案】3.
【解析】
连接AQ,依据等边三角形的性质,即可得到CQ=AQ,依据当A,Q,P三点共线,且AP⊥BC时,AQ+PQ的最小值为线段AP的长,即可得到BP的长.
如图,连接AQ,
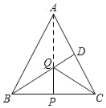
∵等边△ABC中,BD为AC边上的中线,
∴BD垂直平分AC,
∴CQ=AQ,
∴CQ+PQ=AQ+PQ,
∴当A,Q,P三点共线,且AP⊥BC时,AQ+PQ的最小值为线段AP的长,
此时,P为BC的中点,
又∵等边△ABC的周长为18cm,
∴BP=![]() BC=
BC=![]() ×6=3cm,
×6=3cm,
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中,  ,
, 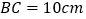 ,点
,点 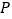 从点
从点 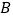 出发,以
出发,以 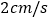 的速度沿
的速度沿 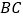 向点
向点 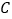 运动,设点
运动,设点 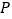 的运动时间为
的运动时间为 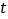 秒:
秒: 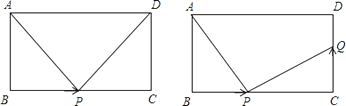
(1)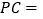
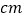 .(用
.(用 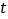 的代数式表示)
的代数式表示)
(2) 当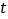 为何值时,
为何值时, 
(3)当点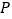 从点
从点 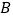 开始运动,同时,点
开始运动,同时,点 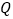 从点
从点 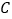 出发,以 v
出发,以 v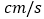 的速度沿
的速度沿 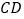 向点
向点 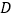 运动,是否存在这样的v 值,使得
运动,是否存在这样的v 值,使得 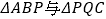 全等?若存在,请求出 v的值;若不存在,请说明理由.
全等?若存在,请求出 v的值;若不存在,请说明理由. -
科目: 来源: 题型:
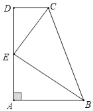
查看答案和解析>>【题目】如图,AB∥CD,∠A=90°,E是AD边的中点,CE平分∠BCD.
(1)求证:BE平分∠ABC;
(2)若AB=2,CD=1,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中错误的是( ).
x
…
-4
-3
-2
-1
0
1
…
y
…
-37
-21
-9
-1
3
3
…
A.当x>1时y随x的增大而增大
B.抛物线的对称轴为x=
C.当x=2时y=-1
D.方程ax2+bx+c=0一个负数解x1满足-1<x1<0 -
科目: 来源: 题型:
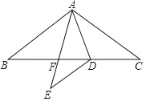
查看答案和解析>>【题目】如图,在△ABC中,点D在BC上,AB=AC=BD,AD=DC,将△ACD沿AD折叠至△AED,AE交BC于点F.
(1)求∠C的度数;
(2)求证:BF=CD.
-
科目: 来源: 题型:
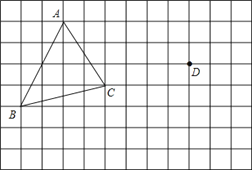
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积=
(2)若连接AD、CF,则这两条线段之间的关系是_________________;
(3)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP.
相关试题

