【题目】某化妆品专卖店,为了吸引顾客,准备在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动,凡购物满![]() 元,均可得到一次摇奖的机会.已知在摇奖机内装有
元,均可得到一次摇奖的机会.已知在摇奖机内装有![]() 个红球和
个红球和![]() 个白球,除颜色外其它都相同,摇奖者必须从摇奖机中一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如下表):
个白球,除颜色外其它都相同,摇奖者必须从摇奖机中一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如下表):

(![]() )请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(![]() )如果一个顾客当天在本店购物满
)如果一个顾客当天在本店购物满![]() 元,若只考虑获得最多的礼品卷,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
元,若只考虑获得最多的礼品卷,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
参考答案:
【答案】(![]() )树状图见解析,
)树状图见解析, ![]() ;(
;(![]() )甲,理由见解析.
)甲,理由见解析.
【解析】试题分析:(1)摇奖机内有两红两白球,标记为红1,红2,白1,白2,连续摇出一红一白,先出来的球有四种情况,且概率相等,分别为红1,红2,白1,白2,画出树状图,再写出后出来球的情况,如上图所示进而找出一红一白的结果有8种,占所有可能出现的结果12种的三分之二.
(2)先在(1)的基础上再算出另外两种情况出现的概率,根据算出的概率,依据甲乙化妆品获得礼品券的方案分别算出获得礼品券,取获得礼品券多的品牌化妆品.
试题解析:(1)用树状图列出所有可能的结果:
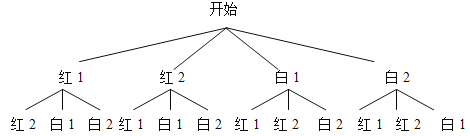
由树状图可知,所有可能出现的结果共有12种,且每种结果出现的可能性相同,其中恰好连续摇出一红一白的结果有8种,所以P(一红一白)=![]() .∴一次连续摇出一红一白两球的概率为
.∴一次连续摇出一红一白两球的概率为![]() .
.
(2)若顾客在本店购物满88元,由(1)得:P(两红)=![]() , P(两白)=
, P(两白)=![]() .
.
(3)若购买甲品牌化妆品,则获得礼品卷为6×![]() +12×
+12×![]() +6×
+6×![]() =10(元);若购买乙品牌化妆品,则获得礼品卷为12×
=10(元);若购买乙品牌化妆品,则获得礼品卷为12×![]() +6×
+6×![]() +12×
+12×![]() =8(元).∵10>8,∴顾客应选择购买甲品牌的化妆品.
=8(元).∵10>8,∴顾客应选择购买甲品牌的化妆品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出两幅不完整的统计图,请根据统计图回答问题.


(1)这次活动一共调查了________名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于________度;
(4)若该学校有1000人,请你估计该学校选择乒乓球项目的学生人数约是________人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进
 、
、 两种新型节能台灯共
两种新型节能台灯共 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:
(
 )若商场预计进货款为
)若商场预计进货款为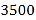 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?(
 )若商场规定
)若商场规定 型台灯的进货数量不超过
型台灯的进货数量不超过 型台灯数量的
型台灯数量的 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是⊙
是⊙ 的直径,弦
的直径,弦 与
与 交于点
交于点 ,过点
,过点 作⊙
作⊙ 的切线与
的切线与 的延长线交于点
的延长线交于点 ,
,  交直线
交直线 于点
于点 .
.(
 )若
)若 ,求证:
,求证:  是⊙
是⊙ 的切线;
的切线;(
 )如果
)如果 ,
,  且
且 为
为 的中点,求直径
的中点,求直径 的长.
的长.
-
科目: 来源: 题型:
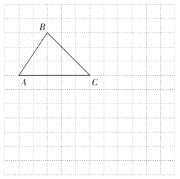
查看答案和解析>>【题目】在平面直角坐标系xOy中,△ABC的三个顶点分别是A(-2,0),B(0,3),C(3,0).
(1)在所给的图中,画出这个平面直角坐标系;
(2)点A经过平移后对应点为D(3,-3),将△ABC作同样的平移得到△DEF,点B的对应点为点E,画出平移后的△DEF;
(3)在(2)的条件下,点M在直线CD上,若DM=2CM,直接写出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“构造图形解题”,它的应用十分广泛,特别是有些技巧性很强的题目,如果不能发现题目中所隐含的几何意义,而用通常的代数方法去思考,经常让我们手足无措,难以下手,这时,如果能转换思维,发现题目中隐含的几何条件,通过构造适合的几何图形,将会得到事半功倍的效果,下面介绍两则实例:
实例一:1876年,美国总统伽非尔德利用实例一图证明了勾股定理:由
S四边形ABCD=S△ABC+S△ADE+S△ABE得
 ,化简得:
,化简得:
实例二:欧几里得的《几何原本》记载,关于x的方程
 的图解法是:
的图解法是:画Rt△ABC,使∠ABC=90°,BC=
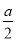 ,AC=
,AC= ,再在斜边AB上截取BD=
,再在斜边AB上截取BD=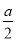 ,则AD的长就是该方程的一个正根(如实例二图)
,则AD的长就是该方程的一个正根(如实例二图)请根据以上阅读材料回答下面的问题:
(1)如图1,请利用图形中面积的等量关系,写出甲图要证明的数学公式是 ,乙图要证明的数学公式是
(2)如图2,若2和-8是关于x的方程x2+6x=16的两个根,按照实例二的方式构造Rt△ABC,连接CD,求CD的长;
(3)若x,y,z都为正数,且x2+y2=z2,请用构造图形的方法求
 的最大值.
的最大值.
相关试题

