【题目】小新的身高是1m,他的影子长为2m,同一时刻水塔的影长是32m,则水塔的高度是m.
参考答案:
【答案】16
【解析】解:设水塔的高为xm, 根据题意得x:32=1:2,解得x=16,
即水塔的高为16m.
所以答案是16.
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列算式:①(a3)2=a3×2=a6;②aman=am+n(m,n为正整数);③[(-x)4]5=-x20.其中正确的算式有( ).
A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列推证过程补充完整.
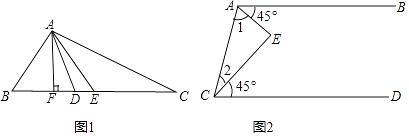
(1)如图1,在△ABC中,AE是中线,AD是角平分线,AF是高.
①BE== ;
;
②∠BAD== ;
;
③∠AFB==90°;
④S△ABC= .
(2)如图2,AB∥CD,∠BAE=∠DCE=45°,
∵AB∥CD
∴∠1+45°+∠2+45°= .
∴∠1+∠2= .
∴∠E= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为5,点P在⊙O内,则下列关系正确的是( )
A.PO>5B.0≤PO<5C.PO=5D.无法判断
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.
(1)求A、B两点的对应的数a、b;
(2)点C在数轴上对应的数为x,且x是方程2x+1=
 x﹣8的解.
x﹣8的解.①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
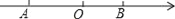
-
科目: 来源: 题型:
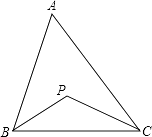
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=60°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度数.
-
科目: 来源: 题型:
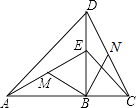
查看答案和解析>>【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由.
相关试题

