【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由. 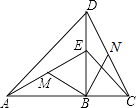
参考答案:
【答案】解:BM=BN,BM⊥BN,
理由是:在△ABE和△DBC中,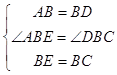 ,
,
∴△ABE≌△DBC(SAS),
∴AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,
∴∠ABD=∠DBC=90°,
∵M为AE的中点,N为CD的中点,
∴BM=AM=EM= ![]() AE,BN=CN=DN=
AE,BN=CN=DN= ![]() CD,
CD,
∴BM=BN,∠EAB=∠MBA,∠CDB=∠DBN,∠AEB=∠EBM,∠NCB=∠NBC,
∵∠EAB=∠BDC,∠AEB=∠DCB,
∴∠ABM=∠DBN,∠EBM=∠NBC,
∴∠ABC=2∠DBN+2∠EBM=180°,
∴∠EBN+∠EBM=90°,
∴BM⊥BN.
【解析】根据SAS推出△ABE≌△DBC,推出AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,求出∠ABD=∠DBC=90°,BM=AM=EM= ![]() AE,BN=CN=DN=
AE,BN=CN=DN= ![]() CD,推出∠ABM=∠DBN,∠EBM=∠NBC即可.
CD,推出∠ABM=∠DBN,∠EBM=∠NBC即可.
【考点精析】本题主要考查了直角三角形斜边上的中线的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小新的身高是1m,他的影子长为2m,同一时刻水塔的影长是32m,则水塔的高度是m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.
(1)求A、B两点的对应的数a、b;
(2)点C在数轴上对应的数为x,且x是方程2x+1=
 x﹣8的解.
x﹣8的解.①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
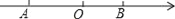
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=60°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度数.
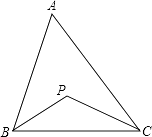
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
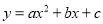 的顶点为
的顶点为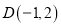 ,其部分图象如图所示,给出下列四个结论:①
,其部分图象如图所示,给出下列四个结论:①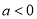 ; ②
; ②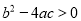 ;③
;③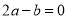 ;④若点
;④若点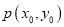 在抛物线上,则
在抛物线上,则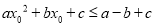 .其中结论正确的是( )
.其中结论正确的是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个凸多边形的内角和与外角和相等,则这个多边形是_________边形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖在二次函数y=2x2+4x+5的图象上,依横坐标找到三点(﹣1,y1),(2,y2),(﹣3,y3),则你认为y1 , y2 , y3的大小关系应为 .
相关试题

