【题目】阅读下列材料,然后回答问题。
在进行二次根式的化简与运算时,我们有时会碰上如![]() ,
,![]() ,
,![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简:
(一) ![]() =
=![]() =
=![]()
(二) ![]() =
=![]()
(三) ![]() =
=![]() =
=![]() 以上这种化简的步骤叫做分母有理化。
以上这种化简的步骤叫做分母有理化。
![]() 还可以用以下方法化简:
还可以用以下方法化简:
(四) ![]() =
=![]()
请用不同的方法化简![]() 。
。
(1)参照(三)式得![]() =_____________________________________;
=_____________________________________;
参照(四)式得![]() =_____________________________________。
=_____________________________________。
(2)化简:![]()
参考答案:
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]()
【解析】
(1)①分子分母同时乘以有理化因式![]() ﹣
﹣![]() ,即可化简;
,即可化简;
②把分子2写成5﹣3,然后利用平方差公式分解,即可化简;
(2)根据上面的例子即可进行化简.
(1)①原式=![]() =
=![]() =
=![]() ﹣
﹣![]() ;
;
②原式=![]() =
=![]() =
=![]() ﹣
﹣![]()
(2)原式=![]() (
(![]() ﹣1+
﹣1+![]() ﹣
﹣![]() +
+![]() ﹣
﹣![]() +…+
+…+![]() ﹣
﹣![]() )=
)=![]() (
(![]() ﹣1).
﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E是AB的中点,AD//EC,∠AED=∠B.

(1)求证:△AED≌△EBC;
(2)当AB=6时,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C.

(1)如图①,若∠A=40°时,点D在△ABC内,则∠ABC+∠ACB= 度,∠DBC+∠DCB= 度,∠ABD+∠ACD= 度;
(2)如图②,改变直角三角板DEF的位置,使点D在△ABC内,请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论.
(3)如图③,改变直角三角板DEF的位置,使点D在△ABC外,且在AB边的左侧,直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.

(1)当直线MN绕点C旋转到图(1)的位置时,显然有:DE=AD+BE;请证明.
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图(3)的位置时,试问(2)中DE、AD、BE的关系还成立吗?若成立,请证明;若不成立,它们又具有怎样的等量关系?请证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
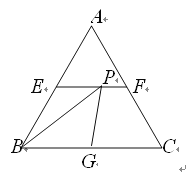
查看答案和解析>>【题目】如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、
AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是
_ ▲ .
相关试题

