Question

【题目】如图，半径为6cm的⊙O中，C、D为直径AB的三等分点，点E、F分别在AB两侧的半圆上，∠BCE=∠BDF=60°，连接AE、BF，则图中两个阴影部分的面积为cm2 ．

Answer 1

【答案】6
【解析】解：如图作△DBF的轴对称图形△CAG，作AM⊥CG，ON⊥CE，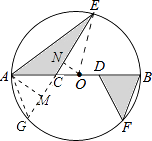
∵△DBF的轴对称图形△CAG，
由于C、D为直径AB的三等分点，
∴△ACG≌△BDF，
∴∠ACG=∠BDF=60°，
∵∠ECB=60°，
∴G、C、E三点共线，
∵AM⊥CG，ON⊥CE，
∴AM∥ON，
∴ ，
在Rt△ONC中，∠OCN=60°，
∴ON=sin∠OCNOC= OC，
∵OC= OA=2，
∴ON= ×2= ，
∴AM=2 ，
∵ON⊥GE，
∴NE=GN= GE，
连接OE，
在Rt△ONE中，NE= = = ，
∴GE=2NE=2 ，
∴S△AGE= GEAM= ×2 ×2 =6 ，
∴图中两个阴影部分的面积为6 ，
所以答案是：6 ．
【考点精析】本题主要考查了含30度角的直角三角形和勾股定理的概念的相关知识点，需要掌握在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．