【题目】如图,已知A(-4,![]() ),B(-1,2)是一次函数y=kx+b与反比例函数y=
),B(-1,2)是一次函数y=kx+b与反比例函数y=![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(m≠0,m<0)图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连结PC、PD,若△PCA和△PDB面积相等,求点P的坐标.
参考答案:
【答案】(1) -4<x<-1;(2) y=![]() x+
x+![]() ,m=-2;(3) 点P的坐标是
,m=-2;(3) 点P的坐标是![]()
【解析】试题分析:(1)观察函数图象得到当-4<x<-1时,一次函数图象都在反比例函数图象上方;
(2)先利用待定系数法求一次函数解析式,然后把B点坐标代入y=![]() 可计算出m的值;
可计算出m的值;
(3)设P点坐标为(x,![]() ,利用三角形面积公式可得到方程,解方程,再得到P的坐标.
,利用三角形面积公式可得到方程,解方程,再得到P的坐标.
试题解析:
(1)当-4<x<-1时,一次函数图象在反比例函数图象上方,故一次函数的值大于反比例函数的值.
(2)设一次函数的解析式为y=kx+b.因为y=kx+b的图象过点(-4,![]() ),(-1,2),则
),(-1,2),则
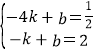
解得![]()
故一次函数的解析式为y=![]() x+
x+![]() .
.
反比例函数y=![]() 图象过点(-1,2),
图象过点(-1,2),
则m=-1×2=-2.
(3)连结PC、PD,设P(x,![]() .由△PCA和△PDB面积相等,得
.由△PCA和△PDB面积相等,得
![]()
解得x=-![]() ,则y=
,则y=![]() x+
x+![]() =
=![]() ,
,
∴点P的坐标是(-![]() ..
..
-
科目: 来源: 题型:
查看答案和解析>>【题目】点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠FAE=∠FAD,FE=FD.
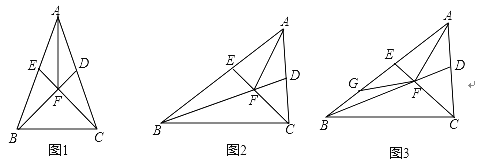
(1)如图1,若∠AEF=∠ADF,求证:AE=AD;
(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;
(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.
-
科目: 来源: 题型:
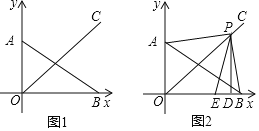
查看答案和解析>>【题目】在平面直角坐标系中,点O为坐标原点,纵坐标为a的点A在y轴上,横坐标为b的点B在x轴上,实数a,b满足|a+b﹣8|+(3a﹣2b+1)2=0
(1)求a,b的值;
(2)如图1,第一象限的点P在∠AOB的平分线OC上,过点P作x轴的垂线,点D为垂足,设线段PD的长为d,△PAB的面积为S(S≠0)用含d的式子表示S,并直接写出相应的d的范围
(3)在(2)的条件下,如图2,当PA⊥PB时,点E在x轴上,连接PE,∠APE=2∠ABO,求PE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x+b与双曲线y=
 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:
(1)
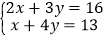 (代入法)
(代入法)(2)
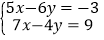 (加减法)
(加减法)(3)
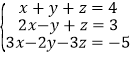
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
-
科目: 来源: 题型:
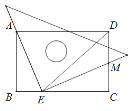
查看答案和解析>>【题目】如图,矩形ABCD中,DE平分∠ADC交BC于点E,将一块三角板的直角顶点放在E点处,并使它的一条直角边过点A,另一条直角边交CD于M点.若点M为CD中点,BC=6,则BE的长为( )
A. 2B.
 C.
C.  D. 3
D. 3
相关试题

